ОГЭ 2020 МАТЕМАТИКА. Задание 16.

6. ОГЭ 2020 МАТЕМАТИКА. Задание 16.

Вариант 01

№16.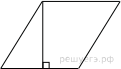

Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Перечислите эти длины в ответе без пробелов в порядке возрастания.

Решение. 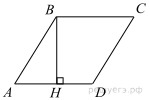Введём обозначения, как показано на рисунке. Имеем:

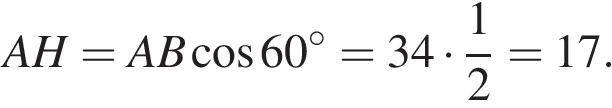
Тогда 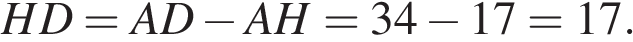Ответ: 1717.

7. ОГЭ 2020 МАТЕМАТИКА. Задание 17.

Вариант 05

№17.

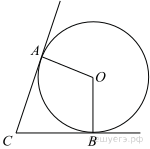
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

Решение.

Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90°. Сумма углов четырёхугольника равна 360°, откуда:

∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 83° = 97°.

Ответ: 97.

Вариант 01

№17. 17 № 340337 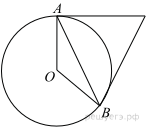Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.

Решение.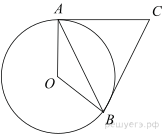

Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому следовательно, треугольник 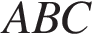— равнобедренный. Откуда 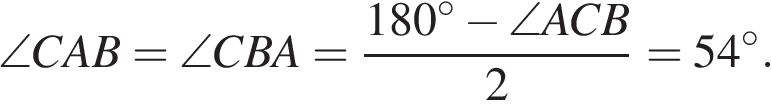Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга 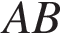равна 108°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно, 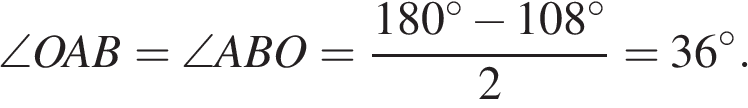Ответ: 36.

Вариант 05

№18. 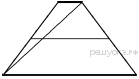Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Решение.

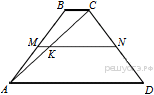Введём обозначения, как показано на рисунке. 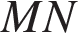— средняя линия, поэтому, откуда по теореме Фаллеса Рассмотрим треугольник 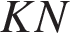— средняя линия, следовательно, 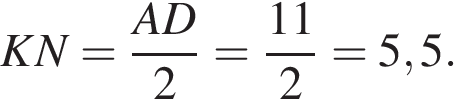Ответ: 5,5.

Домашнее задание: МА_ОГЭ_задания_1-5_вар1

⇐ Предыдущая 1 2 3 45