Таблица 2. Теоретическая часть

Таблица 2

№ опыта	cosφ	φ,°	cosφ_к	φ_к,°	R,Ом	Х_С,Ом	С,Ф	Z_k,Оm	R_k,Ом	X_l,Oм	L_к, Гн

10. Построить в масштабе векторные диаграммы напряжений и тока для всех опытов.

Теоретическая часть

Электрическая цепь переменного тока, так же как и цепь постоянного тока, содержит проводники, по которым перемещаются 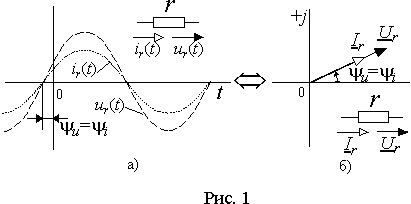электрические заряды. Количество зарядов, проходящих через сечение проводника в единицу времени называется величиной электрического тока. Она зависит от физических свойств и геометрических размеров проводника, а также от разности потенциалов. Связь между этими величинами называется законом Ома.

Закон Ома справедлив всегда, поэтому для любого проводящего участка электрической цепи в любой момент времени можно написать

u = ir = i/g или i = u/r = ug ,

(1)

где u и i - падение напряжения и ток, а r = 1/g и g = 1/r - постоянные коэффициенты, называемые сопротивлением и проводимостью данного участка.

Величина сопротивления определяется коэффициентом, зависящим от свойств проводящей среды и называемым удельным сопротивлением r , а также длиной l и площадью поперечного сечения s участка, в виде r = r l/s. Сопротивление измеряют в омах [Ом] , а обратную ему величину проводимость g в сименсах [См].

Пусть ток в цепи с сопротивлением r изменяется по закону i_r = I_msin(wt+y_i). Тогда в соответствии с выражением (1) падение напряжения в ней будет

u_r = ri_r = rI_msin(wt+y_i) = U_msin(wt+y_u) .

(2)

Отсюда следует, что начальные фазы тока и напряжения на этом участке одинаковы y_i = y_u , а амплитуда напряжения равна U_m = rI_m. Временные диаграммы, соответствующие выражению (2) приведены на рис. 1 а). Там же показано изображение сопротивления на электрических схемах с условно положительными направлениями тока и напряжения.

Амплитудные и действующие значения синусоидальных величин связаны между собой постоянным коэффициентом, поэтому для действующих значений тока и напряжения на сопротивлении можно написать U = rI или I = U/r = gU .

Синусоидальные функции выражения (2) можно заменить комплексными числами

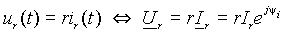
(3)

и изобразить их на векторной диаграмме рис. 1б) с соответствующим представлением на схеме.

Падение напряжения, вызванное протеканием тока, возникает на всех участках электрической цепи. Однако при расчетах его принято изображать отдельным элементом называемым сопротивлением или резистором.

В электрических цепях с синусоидальными переменными токами и напряжениями помимо статических явлений, свойственных цепям постоянного тока, появляются динамические эффекты, т.е. эффекты связанные с изменением этих величин во времени.

Так на любом участке электрической цепи, по которому протекает переменный ток будет действовать ЭДС самоиндукции e_L, наводимая изменяющимся во времени магнитным потоком и равная

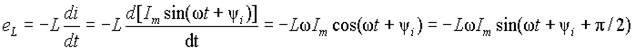(4)

Магнитный поток обязательно охватывает все участки электрической цепи, следовательно, при переменном токе на всех участках будет возникать дополнительное падение напряжения

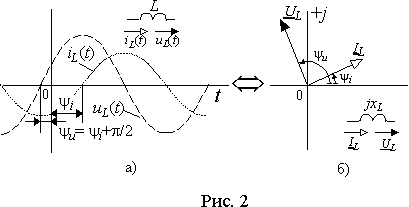
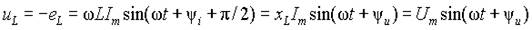(5)

где величина x_L=w L , имеющая размерность сопротивления, называется индуктивным сопротивлением. Амплитуда напряжения, возникающего за счет ЭДС самоиндукции, равна U_m=x_LI_m , а его начальная фаза y _u = y _i +p /2 больше начальной фазы протекающего тока на p /2, т.е. напряжение опережает по фазе ток на 90° . Временные диаграммы, соответствующие выражению (5), приведены на рис. 2 а).

Из выражения для амплитуды падения напряжения на индуктивности можно определить его действующее значение U_L=x_LI_L или действующее значение тока I_L=U_L/x_L=b_LI_L, где b_L=1/x_L называется индуктивной проводимостью.

Индуктивное сопротивление по сути своей является распределенным параметром, т.к. магнитный поток существует везде, где протекает электрический ток, и на всех участках электрической цепи будет наводиться ЭДС самоиндукции, пропорциональная соответствующему индуктивному сопротивлению. Однако на практике индуктивность всей цепи или отдельного участка считают сосредоточенной в отдельном элементе, изображаемом на схемах в виде рис. 2 а).

Выражение (5) можно представить через символические комплексные числа в виде:

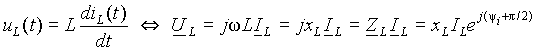(6)

где Z_L=jx_L=x_Le ^jp^/2 - комплексное индуктивное сопротивление.

Векторная диаграмма и схема замещения для выражения (6) приведены на рис. 2 б).

Из выражения (6) можно определить комплексное значение тока через падение напряжения

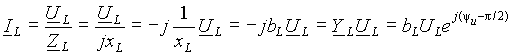(7)

где Y_L=1/Z_L=1/jx_L= - jb_L =b_Le - ^jp^/2 - комплексная индуктивная проводимость.

Из курса физики известно, что заряд уединенного проводящего тела q пропорционален его потенциалу u, т.е. q = Cu . Коэффициент пропорциональности C между зарядом и потенциалом называется емкостью и при неизменных геометрических размерах и свойствах среды является константой. Емкость измеряется в фарадах [Ф] . Фарада является слишком крупной величиной, поэтому для практических целей пользуются ее десятичными долями: микро-, нано- и пикофарадами (10^-6, 10^-9 и 10^-12 Ф).

Если за бесконечно малый промежуток времени dt заряд тела изменился на величину dq , то изменение потенциала за этот же интервал времени составит du=dq/C или dq=Cdu . Отнесем изменение заряда к промежутку времени, за который оно произошло. Тогда с учетом того, что электрический ток есть скорость изменения заряда, т.е. i=dq/dt, получим

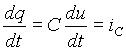. (8)

Пусть напряжение на емкости изменяется во времени по синусоидальному закону u_С = U_msin(wt+y_u). Тогда из выражения (8) ток в емкости определится в виде

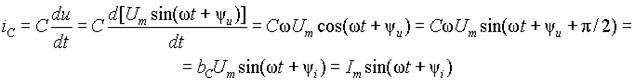. (9)

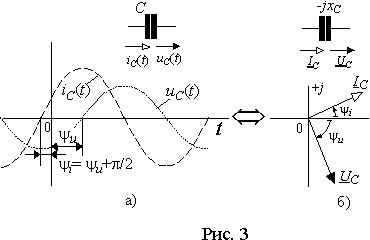
Произведение b_C= wC имеет размерность проводимости [1/Ом=См] и называется емкостной проводимостью. Отсюда амплитуда тока I_m=b_CU_m , а его начальная фаза y _i = y _u + p /2 . Таким образом, ток в емкости опережает падение напряжения на ней на 90° . Временные диаграммы, соответствующие этим соотношениям тока и напряжения на емкости приведены на рис. 3 а).

Пользуясь связью между амплитудными и действующими значениями, для действующих значений тока и падения напряжения на емкости можно записать I_С=b_CU_С или U_C=I_C/b_C=x_CI_C , где величина x_C=1/b_C называется емкостным сопротивлением.

При описании электромагнитных процессов в электрических цепях часто требуется выражение для мгновенного значения напряжения на емкости. Его можно получить из выражения (8) в виде

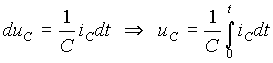. (10)

Из выражения (8) следует, что всякое изменение потенциалов в электрической цепи будет вызывать появление токов, приводящих к перераспределению зарядов. Причем, под токами в этом процессе следует понимать как токи проводимости, так и токи смещения, возникающие между всеми участках цепи. Поэтому емкостная проводимость, как и емкость, является распределенным параметром, но для расчетов ее, аналогично индуктивности, представляют сосредоточенной в отдельном элементе, который изображается на схеме в виде рис. 3 а).

Связь между напряжением и током в емкости можно представить также комплексными числами и соответствующими векторами (рис. 3 б)) в виде

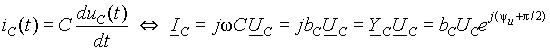, (11)

где Y_C=jb_C=b_Ce ^jp^/2 - комплексная емкостная проводимость.

Отсюда можно также определить комплексное падение напряжения на емкости

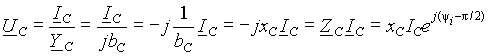, (12)

где Z_C=1/Y_C=1/jb_C= - jx_C = x_Ce - ^jp^/2 - комплексное емкостное сопротивление.

Индуктивность L и емкость C называютсяреактивными элементами электрической цепи. Реактивными называются также соответствующие сопротивления и проводимости. Это связано с тем, что падение напряжения на индуктивности и ток через емкость появляются только как следствие или реакция на изменение тока или разности потенциалов.

В резисторе падение напряжения не связано с изменением тока, поэтому его сопротивление, в отличие от реактивного, называется активным или резистивным

⇐ Предыдущая 1 234 5 Следующая ⇒