
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.
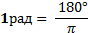 ;
;
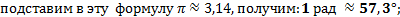
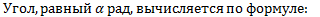 α рад=(180/π α)°(1)
α рад=(180/π α)°(1)
Длину дуги l окружностирадиуса R (рис.4)

можно вычислять по формуле 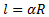 (3)
(3)
А площадь S кругового сектора радиуса R и дугой 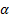 рад (рис.5)
рад (рис.5)
находят по формуле:  , где
, где  (4)
(4)
Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки.(рис.2)
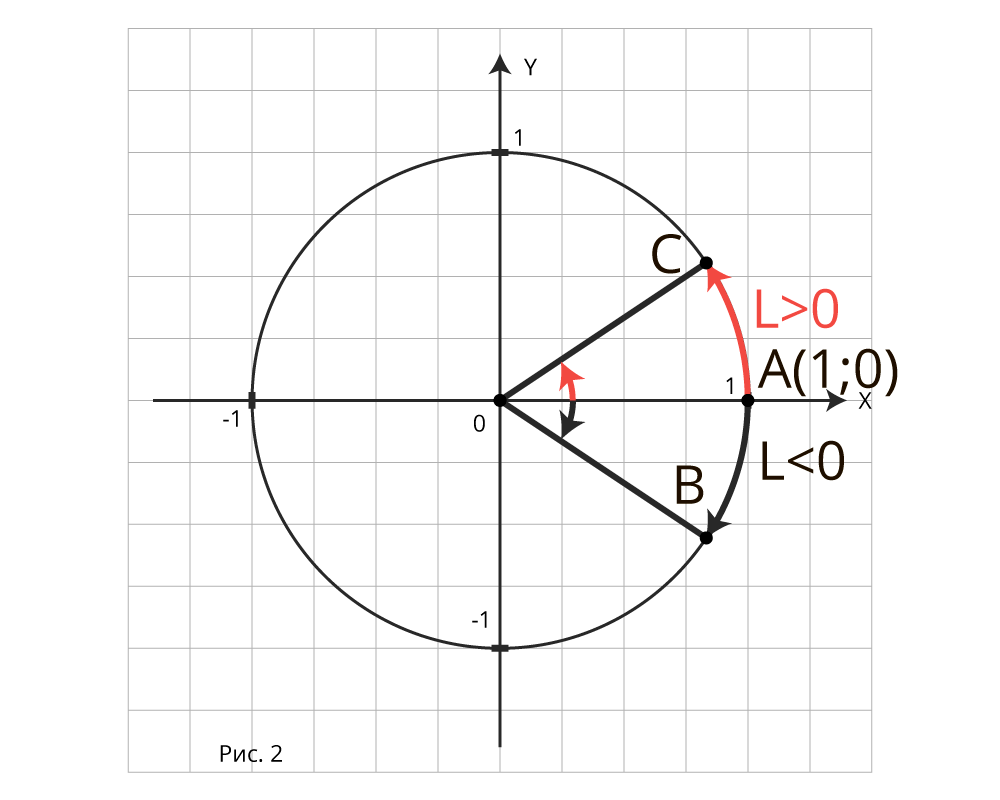
1. Пусть 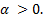 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 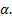
2. Пусть  точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол - α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол - α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол 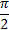 получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
угол 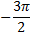 (рис.6)
(рис.6)
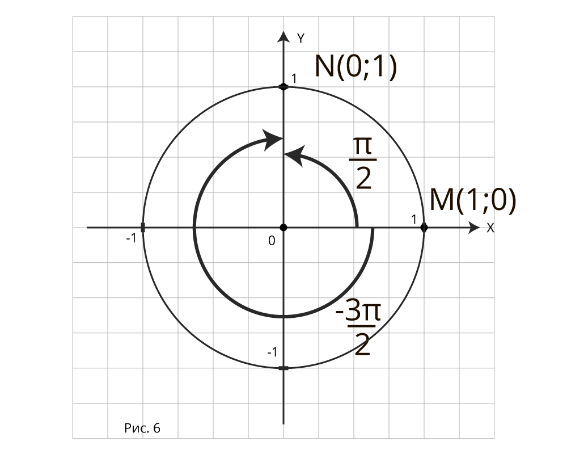
(рис.6)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найти градусную меру угла, равного 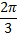 рад.
рад.
Решение: Используя формулу (1),
находим 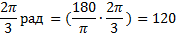 .
.
Так как 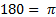 , то
, то 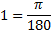 рад, тогда
рад, тогда 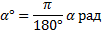 (2)
(2)
Ответ: 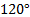 .
.
Пример 2. Найти радианную меру угла, равного 60 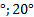 .
.
Решение:
Вычисляем по формуле (2): 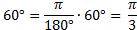 рад
рад
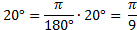 рад
рад
При обозначении мер угла, наименование «рад» опускают.
Ответ:  рад,
рад,  рад.
рад.
Пример 3.Найти длину дуги окружности радиуса 6 см, если её радианная мера 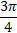 .
.
Решение: Используя формулу (3),
получим: 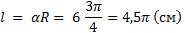
Ответ: 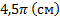 .
.
Пример 4.Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла 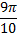 .
.
Решение:
По формуле (4) вычисляем 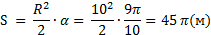
Ответ: 45 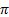 м2
м2
Пример 5.Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный  .
.
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как 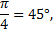 то
то
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны 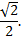 Учитывая, что точка М находится в I координатной четверти, её координаты положительны.
Учитывая, что точка М находится в I координатной четверти, её координаты положительны. 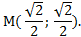
На окружности можно найти координаты любой точки.
Ответ: 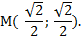
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|