
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание: изучить материал урока, записать решения разобранных задач и выполнить домашнее задание.
Задание: изучить материал урока, записать решения разобранных задач и выполнить домашнее задание.
Информационная карта к уроку
по теме: Применение производной к исследованию функций на наибольшее и наименьшее значение.
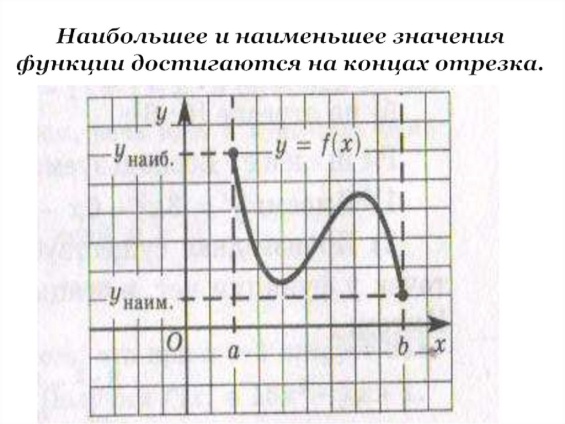
Ход урока
Определите по рисунку и сравните максимум с наибольшим значением, минимум с наименьшим значением функции.
Вы видите, что функция на концах промежутка может достигать значение большее максимума, и меньшее минимума.
Таким образом, для нахождения наименьшего значения функции нужно сравнить значения в точках минимума и на концах отрезка, а для нахождения наибольшего значения функции нужно сравнить значения в точках максимума и на концах отрезка. Для этого выделим следующий алгоритм:
1. Найти значения функции на концах отрезка, т.е. числа f(a) и f(b)
2. Найти критические точки.
3. Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b)
4. Из всех найденных значений выбрать наибольшее и наименьшее
Однако, в зависимости от того, как себя ведет функция на отрезке, этот алгоритм можно изменить.
Примеры: 1. Задание. Найдите наибольшее значение функции 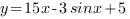 на отрезке
на отрезке 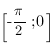 .
.
1. Функция 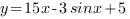 определена при всех действительных значениях х
определена при всех действительных значениях х
2. 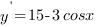
3. 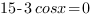
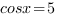 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция 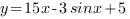 возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|