Бесконечно малая функция при 𝑥→𝑎 является ограниченной в некоторой окрестности точки 𝑎.

2. Бесконечно малая функция при 𝑥→𝑎 является ограниченной в некоторой окрестности точки 𝑎.

Доказательство. По определению бесконечно малой функции при 𝑥→𝑎 : ∀𝜀>0 ∃𝛿>0: ∀𝑥, 0<|𝑥−𝑎|<𝛿, |𝛼(𝑥)|<𝜀 .Иначе –𝜀<𝛼(𝑥)<𝜀 в окрестности точки а радиуса 𝛿 (дельта).Значит функция ограничена в интервале (–𝜀;𝜀).

3. Произведение бесконечно малой функции при 𝑥→𝑎 и функции, ограниченной в некоторой окрестности точки 𝑎, есть бесконечно малая функция при 𝑥→𝑎.

Доказательство. Пусть- 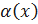– БМФ при 𝑥→a и f(x) – ограниченная функция в некоторой окрестности точки а. Рассмотрим функцию вида 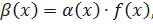когда 𝑥→a. Для любого 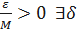такое, что 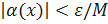, как только х попадет в 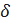– окрестность точки а, то есть 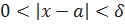. Кроме того, так как 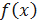ограничена в некоторой окрестности точки а, то найдется такое М>0, что можно записать 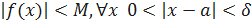. Следовательно, 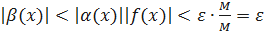ч.т.д.

4. Произведение нескольких БМФ есть БМФ.

Доказательство. Непосредственно следует из определения

5. Произведение БМФ на постоянную есть БМФ.

Доказательство. На основе свойства 3.

⇐ Предыдущая 12