
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Границы и грани числовых множеств.Существование точной верхней и точной нижней граней числовых множеств.
БИЛЕТ 4
Границы и грани числовых множеств.Существование точной верхней и точной нижней граней числовых множеств.



Бесконечно малые функции при 𝑥→𝑎 (различные формулировки),геометрический смысл,примеры бесконечно малых функций при 𝑥→𝑎. Теорема о свойствах бесконечно малых функций при 𝑥→𝑎.
1. Бесконечно малые функции
Определение (1). Функция 𝛼(𝑥) называется бесконечно малой при 𝑥→𝑎 (БМФ), если ∀𝜀>0 ∃𝛿>0: ∀𝑥, 0<|𝑥−𝑎|<𝛿, |𝛼(𝑥)|<𝜀. 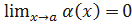
Определение предела функции через окрестность (2)
Функция 𝛼(𝑥) является бесконечно малой при 𝑥 → 𝑎 тогда и только тогда, когда ∀𝜀>0 ∃𝛿>0, что как только x попадает в выколотую дельта-окрестность точки 𝑎, соответствующее значение функции 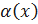 попадает в -окрестность числа ноль.
попадает в -окрестность числа ноль.
2.Примеры бесконечно малых функций
Функция 𝑦=𝑥2 является бесконечно малой при 𝑥→0, но не является бесконечно малой при 𝑥→1. В самом деле, 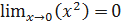 , а
, а 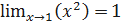 .
.
- Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
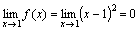 (см. рис.).
(см. рис.). - Функция f(x) = tgx – бесконечно малая при x→0.
- f(x) = ln (1+x)– бесконечно малая при x→0.
- f(x) = 1/x– бесконечно малая при x→∞.
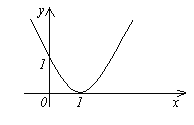 3.Геометрический смысл
3.Геометрический смысл
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если 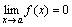 или
или 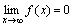 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
4. Теорема о свойствах бесконечно малых функций при 𝑥→𝑎. (БМФ)
1. Сумма любого конечного числа БМФ есть БМФ.
Доказательство. Достаточно доказать это свойство для двух функций. Итак, пусть 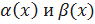 – БМФ при 𝑥→a. Тогда для любого
– БМФ при 𝑥→a. Тогда для любого 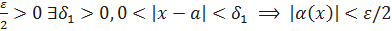 и
и 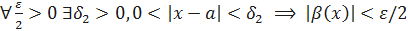 . Рассмотрим выражение
. Рассмотрим выражение 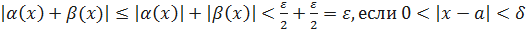 , где
, где 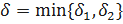 . А это означает, по Коши, что
. А это означает, по Коши, что 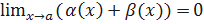 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|