Раздел 2 Решить с помощью подпрограммы – процедуры

Раздел 2 Решить с помощью подпрограммы – процедуры

1. Заданы два вектора х = (x1, x2, x3, x4), y = (y1, y2, y3, y4). Определить угол a между векторами x и y по формуле: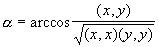

Вычисление скалярного произведения оформить в виде процедуры.

2. Четыре точки заданы своими координатами X(x1, x2), Y(y1, y2), Z(z1, z2), P(p1, p2). Выяснить, какие из них находятся на максимальном расстоянии друг от друга и вывести на печать значение этого расстояния. Вычисление расстояния между двумя точками оформить в виде процедуры.

3. Четыре точки заданы своими координатами X(x1, x2, x3), Y(y1, y2, y3), Z(z1, z2, z3), T(t1, t2, t3).Выяснить, какие из них находятся на минимальном расстоянии друг от друга и вывести на печать значение этого расстояния. Вычисление расстояния между двумя точками оформить в виде процедуры.

4. Три точки заданы своими координатами X(x1, x2), Y(y1, y2) и Z(z1, z2). Найти и напечатать координаты точки, для которой угол между осью абсцисс и лучом, соединяющим начало координат с точкой, минимальный. Вычисления оформить в виде процедуры.

5. Задана окружность (x-a)² + (y-b)² = R² и точки Р(р1, р2), F(f1, f2), L(l1, l2). Выяснить и напечатать, сколько точек лежит внутри окружности. Проверку, лежит ли точка внутри окружности, оформить в виде процедуры.

6. Заданы три матрицы А(второго порядка), В(третьего порядка) и С(четвертого порядка). Выяснить и напечатать, сколько из них являются симметричными (Матрица называется симметричной, если транспонированная матрица равна исходной). Транспонирование матрицы оформить в виде процедуры.

7. Заданы матрицы А и В третьего порядка. Переменной S присвоить -1, если максимальный элемент матрицы А больше максимального элемента матрицы В; 0 если максимальные элементы матрицы равны; 1, если максимальный элемент матрицы А меньше максимального элемента матрицы В. Поиск максимального элемента оформить в виде процедуры.

8. Заданы два вектора X(x1,x2,x3), Y(y1,y2,y3) и матрица А третьего порядка. Найти сумму двух векторов c и d, где вектор с есть произведение вектора x на матрицу А, а вектор d - произведение вектора на матрицу А. Вычисление произведения вектора на матрицу оформить в виде процедуры.

9. Заданы три матрицы А(третьего порядка), В(второго порядка) и С(третьего порядка). Найти максимальное из трех чисел x, y, z, где x - след матрицы А, у- след матрицы В, z- след матрицы С.(Следом матрицы называется сумма элементов главной диагонали). Вычисление следа матрицы оформить в виде процедуры.

10. Даны отрезки а, b, c и d. Для каждой тройки этих отрезков, из которой можно построить треугольник, вывести на экран площадь данного треугольника. Проверку существования треугольника оформить в виде процедуры.

11. Даны длины сторон треугольника a, b, c. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Для вычисления медианы проведенной к стороне а, использовать формулу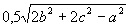

Вычисление медианы оформить в виде процедуры.

12. Даны две матрицы размером 3x3. Написать программу получения коммутатора АВ-ВА и антикоммутатора АВ+ВА этих матриц. Вычисление произведения матриц оформить в виде процедуры.

13. Дана квадратная матрица А. Написать программу вычисления матрицы Ат*Ат*А*А, Ат - транспонированная матрица. Вычисление произведения матриц оформить в виде процедуры.

14. Даны две матрицы А и В. Написать программу, меняющую местами максимальные элементы этих матриц. Нахождение максимального элемента матрицы оформить в виде процедуры.

15. Даны три квадратные матрицы третьего порядка. Вывести на экран ту из них, норма которой наименьшая. В качестве нормы матрицы взять максимум модулей ее элементов. Нахождение нормы матрицы оформить в виде процедуры.

16 Заданы четыре вектора : X = {x1, x2, x3}, Y = {y1, y2, y3}, Z = {z1, z2, z3, z4}, P = {p1, p2, p3, p4}. Логической переменной a присвоить значение true, если скалярное произведение векторов X и Y больше скалярного произведения Z и P, значение false в противном случае. Нахождение скалярного произведения оформить в виде процедуры.

17 Описать процедуру Sort(A, B, C), меняющую содержимое переменных A, B, C таким образом, чтобы их значения оказались упорядоченными по убыванию (A, B, C — вещественные параметры, являющиеся одновременно входными и выходными). С помощью этой процедуры упорядочить по убыванию два данных набора из трех чисел: (A1, B1, C1) и (A2, B2, C2).

18 Описать процедуру Mean(X, Y, AMean, GMean), вычисляющую среднее арифметическое AMean = (X + Y)/2 и среднее геометрическое GMean = (XY)^1/2⋅двух положительных чисел X и Y (X и Y — входные, AMean и GMean — выходные параметры вещественного типа). С помощью этой процедуры найти среднее арифметическое и среднее геометрическое для пар (A, B), (A, C), (A, D), если даны A, B, C, D.

19 Описать процедуру RectPS(x1, y1, x2, y2, P, S), вычисляющую периметр P и площадь S прямоугольника со сторонами, параллельными осям координат, по координатам (x1, y1), (x2, y2) его противоположных вершин (x1, y1, x2, y2 — входные, P и S — выходные параметры вещественного типа). С помощью этой процедуры найти периметры и площади трех прямоугольников с данными противоположными вершинами.

20 Описать процедуру DigitCountSum(K, C, S), находящую количество C цифр целого положительного числа K, а также их сумму S (K — входной, C и S — выходные параметры целого типа). С помощью этой процедуры найти количество и сумму цифр для каждого из пяти данных целых чисел.

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒