Контакты

Случайная статья

Тема: Формулы объема и площади поверхностей усечённых пирамиды и конуса.

Стр 1 из 3Следующая ⇒

Тема: Формулы объема и площади поверхностей усечённых пирамиды и конуса.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава VII, § 3, п. 80-81), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.

Теоретический минимум и задачи

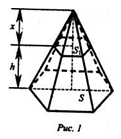
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).

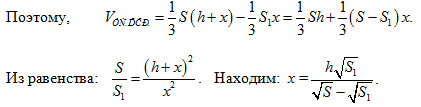
Подставим это выражение для х в первую формулу,

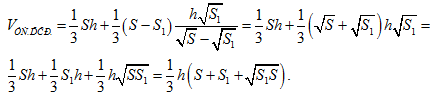
Объем усеченного конуса

Усеченный конус можно получить, вращая прямоугольную трапецию 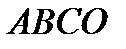вокруг оси .

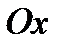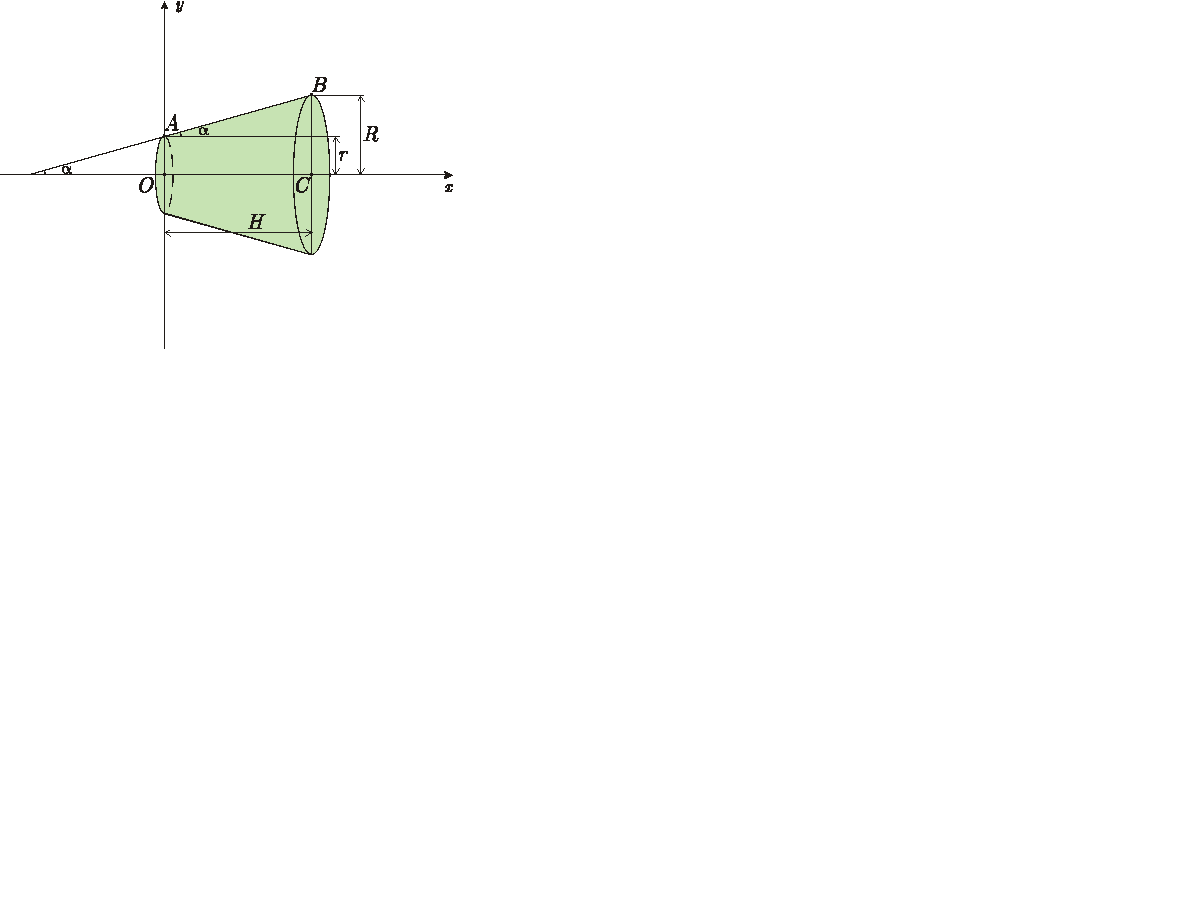Найдем уравнение прямой 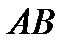, образующей коническую поверхность. Для этого положим 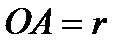, , 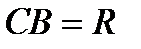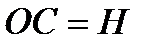и напишем уравнение в виде , , .

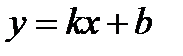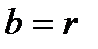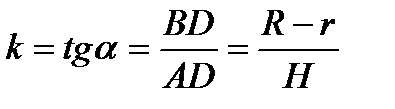Таким образом, искомое уравнение будет: .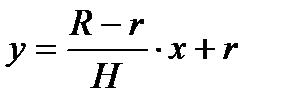

Согласно формуле 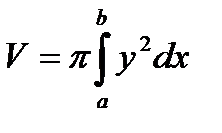, найдем: .

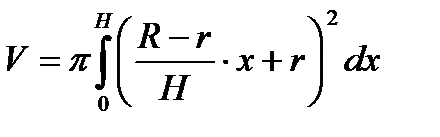Вычислим определенный интеграл способом подстановки. Положим 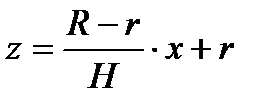. Тогда 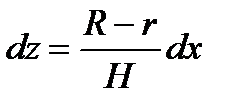. Отсюда 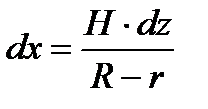. Новыми пределами интеграла будут: , .

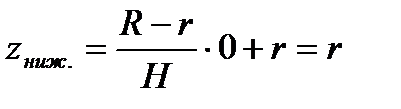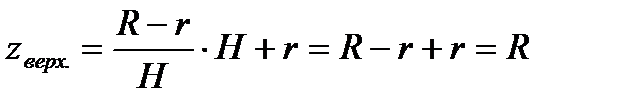Следовательно,

.

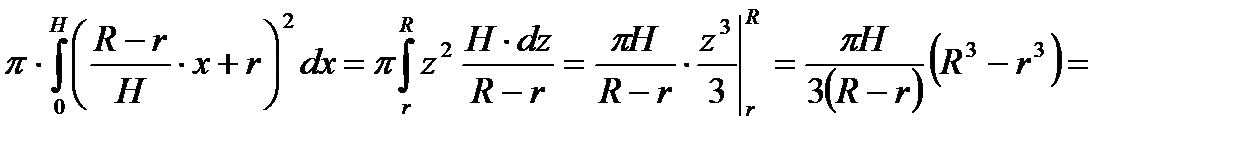
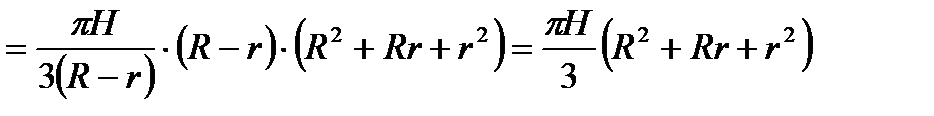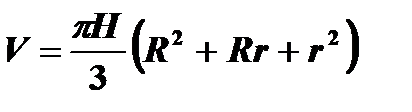
Площадь боковой поверхности правильной усечённой пирамиды: Sбок.= (P1+P2)⋅h, где P1и P2−периметры оснований.

Площадь боковой поверхности усеченного конуса.

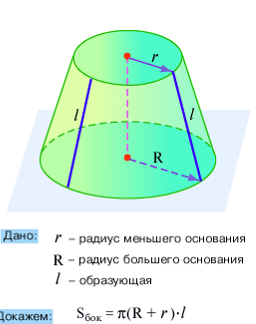
Рассмотрим решение задач.

Задача 1

12 3 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.