Область определения функции D(y) симметрична относительно точки О

Свойства функций.

Изучение свойств функций имеет большое значение для исследования функций и построения их графиков. Геометрическая интерпретация свойств функций играет большую роль для последующего правильного восприятия и осмысления графиков физических и многих других процессов.

Рассмотрим функции, области определения которых симметричны относительно начала координат. Среди таких функций выделяются четные и нечетные.

Область определения функции D(y) симметрична относительно точки О

Определение 1: Функция f(x) называется четной, если для любого х из области определения выполняется равенство:
f(-x)= f(x)

График четной функции симметричен относительно оси Оу.

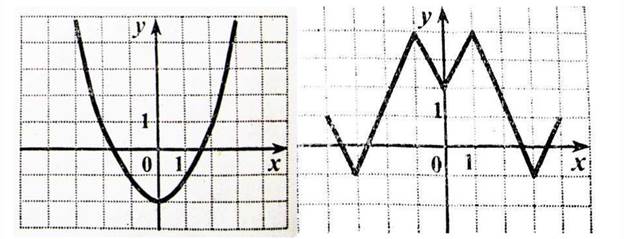
Определение 2: Функция f(x) называется нечетной, если для любого х из области определения выполняется равенство:
f(-x)= - f(x)

График нечетной функции симметричен относительно точки О.

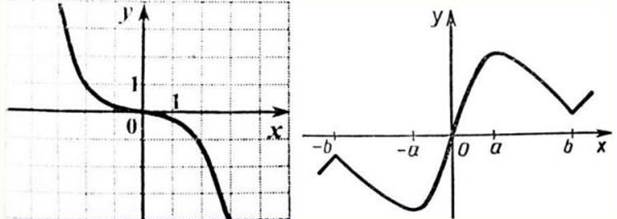
Пример 1:

Является функция четной или нечетной?

1) у=3х²+х⁴
Найдем f(-x)= 3(-х)²+(-х)⁴=3х²+х⁴=f(x), следовательно, f(x) – четная

2) у=х(5-х²)
Найдем f(-x)= -х(5-(-х)²)= -х(5-х²)= - f(x), следовательно, f(x) – нечетная

3) у=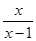
Т.К. область определения функции D(y)=(-¥,1) È(1, +¥) не симметрична относительно точки О, функция не является ни четной, ни нечетной.

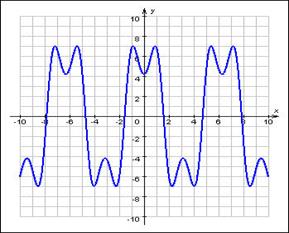
Многие процессы и явления, с которыми мы встречаемся на практике, имеют повторяющийся характер. Такие процессы называют периодическими, а функции, которые их описывают, называют периодическими.

Определение 3: Функция f(x) называется периодической, если для любого х из области определения выполняется равенство:
f(x+Т)= f(x), где Т – период функции.

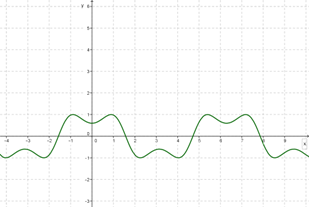
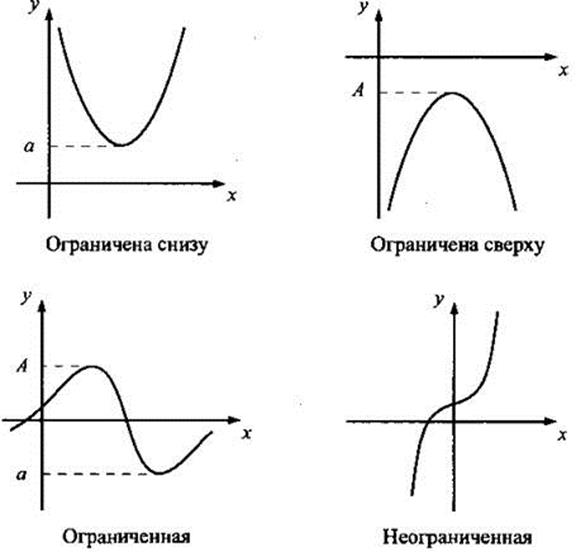
Определение 4: Если модуль функции при любых значениях аргумента не превосходит какого-либо положительного числа, то функция называется ограниченной.

12 Следующая ⇒