Применение основных равносильностей алгебры высказываний для решения содержательных задач

В качестве примера докажем, что , например, формулы и являются тождественно истинными (тавтологиями), построив для их левых и правых частей таблицы истинности и используя табличные определения основных логических операций

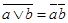
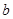
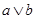
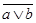
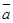
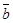
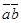
В четвертом и седьмом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула является тавтологией.

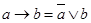
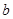
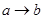
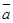
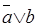
В третьем и пятом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула также является тавтологией.

11. 2. Применение основных равносильностей алгебры высказываний для решения содержательных задач

Рассмотрим на примере, как используются приведенные выше равносильности алгебры высказываний при решении содержательных задач.

Задача: В замке есть две комнаты, в каждой из которых может находиться либо тигр, либо принцесса. На дверях комнат имеются таблички следующего содержания: табличка I - «По крайней мере в одной из комнат находится принцесса», табличка II – «Принцесса находится в другой комнате».

Если в первой комнате находится принцесса, то утверждение на табличке I истинно, если тигр – то ложно. Для второй комнаты наоборот, если там находится принцесса, то утверждение на табличке II ложно, а если там находится тигр – то это утверждение истинно. Определить, в какой из комнат находится принцесса.

Решение:

Введем обозначения для простых высказываний, необходимые для формализации условия задачи, обозначив соответственно через П1 высказывание «принцесса находится в первой комнате», через П2 - высказывание «принцесса находиться во второй комнате», тогда высказывание «тигр находится в первой комнате» есть отрицание переменной П1, а высказывание «тигр находится во второй комнате» - отрицание высказывания П2.

Тогда надпись на первой двери (обозначим это сложное суждение через А) можно представить в виде конъюнкции высказываний П1 и П2 (А=П1 П2), а надпись на второй двери (обозначим его через В) совпадает с высказыванием П1, т.е. В=П1.

Учитывая условие, что при нахождении в первой комнате принцессы утверждение на табличке I истинно, тигра – то ложно, а для второй комнаты при нахождении в ней принцессы утверждение на табличке II ложно, нахождения в ней тигра это утверждение истинно, получим в формализованном виде следующую запись условия нашей задачи:

(П1*А П1*А)*(П2*В П2*В)=

=(П1*(П1 П2) П1* (П1 П2))(П2*П1 П2*П1)=

=П1* П2.

1. П1*(П1 П2) П1* (П1 П2)= П1*П2 П1 П1* П1*П2=

= П1*П2 П1 П1*П2=П1 П2;

2. (П2*П1 П2*П1)* (П1 П2) =

= П2*П1*П1 П2*П1*П2 П2*П1*П1 П2*П1*П2=

= П1* П2.

Замечание: жирным шрифтом здесь отмечены нулевые конъюнкции, - знак операции дизъюнкция, * - знак операции конъюнкция, - знак операции отрицания.

С учетом введенных обозначений для переменных П1 и П2 (П1- «принцесса находится в первой комнате», П2 – «принцесса находится во второй комнате») и полученной в результате преобразований формуле П1* П2 можем сформулировать ответ на вопрос задачи – принцесса находится в первой комнате.

⇐ Предыдущая 12