Задача. Подсказка 1. Подсказка 2. Решение

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Задача

а) Докажите, что любым треугольником можно замостить плоскость.

б) Докажите, что любым четырёхугольником (как выпуклым, так и невыпуклым) можно замостить плоскость.

в) Приведите пример пятиугольника, которым можно замостить плоскость.

г) Приведите пример шестиугольника, которым нельзя замостить плоскость.

д) Приведите пример n-угольника для какого-либо n > 6, которым можно замостить плоскость.

Подсказка 1

В пунктах а), в), д) можно попытаться составить из одинаковых фигур «полоски», которыми потом легко замостить всю плоскость.

Пункт б): сложите из двух одинаковых четырехугольников шестиугольник, у которого противоположные стороны попарно параллельны. Такими шестиугольниками замостить плоскость уже достаточно просто.

Пункт г): используйте тот факт, что сумма углов при каждой вершине должна быть равна 360°.

Подсказка 2

В пункте д) можно попробовать действовать и по-другому: немного менять уже имеющиеся фигуры, чтобы получались новые замощения.

Решение

Примеры ответов изображены на рисунках.

а):

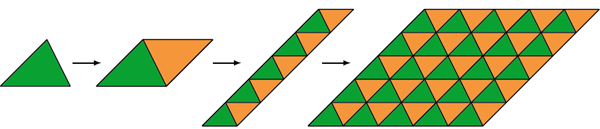Рис. 2

б):

Рис. 3

в) Подойдет пятиугольник в форме домика:

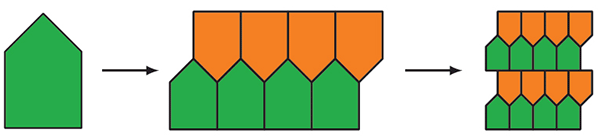Рис. 4

г) Такими шестиугольниками плоскость замостить не получится: в «вырезанный» угол просто не влезет полностью никакая часть такого шестиугольника. По клеточкам это хорошо видно:

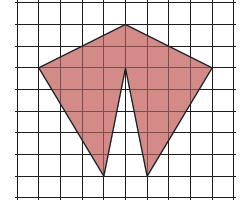Рис. 5

Можно придумать еще множество других шестиугольников, которыми нельзя замостить плоскость.

д) Вот пример двенадцатиугольника, которым можно замостить плоскость. Этот способ замощения получен как модификация обычной квадратной решетки (см. рис. 1, ii из условия):

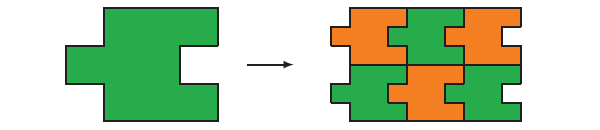Рис. 6

⇐ Предыдущая 123 Следующая ⇒