
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рабочий лист.. Тема урока: Применение векторов вычисления величин расстояний, углов. 1.Понятие угла между векторами.. Формула вычисления угла между векторами.
Урок № 89-90.
Рабочий лист.
| Предмет | Математика |
| Группа | № 37 1курс |
| Тема урока | Применение векторов вычисления величин расстояний, углов. |
| ФИО преподавателя | Тимиршина Алия Мунзиловна |
| Где находится задание: | |
| Учебник | Математика: учебник для учреждений нач.и сред. проф.образования/ М.И. Башмаков, Математика: задачник для учреждений нач.и сред. проф.образования/ М.И. Башмаков Алгебра и начала анализа: А.Н. Колмогоров |
| Ссылка | 1. https://may.alleng.org/d/math-stud/math-st876.htm 2. http://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf 3. http://lib.maupfib.kg/wp-content/uploads/2015/12/Algebra_i_nachala_mat_analiz.pdf |
| Сроки выполнения задания | 15.05.2021 до 17:00 часов |
| Как выполнять задание | Написать конспект, выполнить контрольную работу. |
| Домашняя работа | |
| Обратная связь | Выполненные работы отправить личным сообщением ВК , после просмотра задания поставьте лайк, чтобы зафиксировать посещаемость. |
| Как узнать отметку о выполненном задании | Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК. |
Тема урока: Применение векторов вычисления величин расстояний, углов. 1.Понятие угла между векторами.
Угол между векторами - это угол между их направлениями (рис.1).
Угол между сонаправленными векторами равен 0.
Угол между противоположно направленными векторами равен 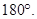
Угол между ортогональными векторами равен 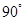 .
.
2. Формула вычисления угла между векторами.
Из определения скалярного произведения векторов находим угол
между векторами:
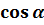 =
= 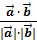 ;
; 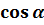 =
= 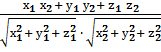 .
.
Пример 1.Найдите угол АСВ в треугольнике АВС, если 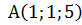 , В(-2;0;7) и С(-3;-2;5).
, В(-2;0;7) и С(-3;-2;5).
Решение. 1. Угол АСВ в треугольнике АВС находится между векторами 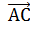
и 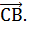 Определим координаты векторов:
Определим координаты векторов: 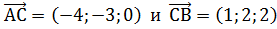 .
.
2. Найдём угол между векторами 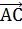 и
и 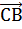 по формуле (1), подставив в неё соответствующие координаты:
по формуле (1), подставив в неё соответствующие координаты:
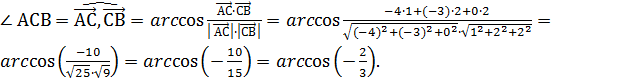
3. Определим величину искомого угла 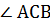 по таблице значений тригонометрических функций или с помощью калькулятора:
по таблице значений тригонометрических функций или с помощью калькулятора: 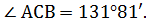
Итак, угол между векторами 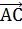 и
и 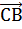 найден:
найден: 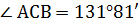 .
.
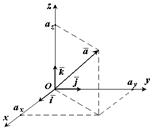 3.Понятие направляющих косинусов вектора.
3.Понятие направляющих косинусов вектора.

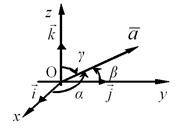 4.Формулы вычисления направляющих косинусов вектора.
4.Формулы вычисления направляющих косинусов вектора.
Определим углы, составляемые вектором AB = (x; y; z) с координатными осями:
с осью ОХ : 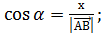
с осью ОY : 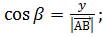
с осью ОZ : 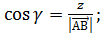
Пример 2.Найти углы, составляемые вектором 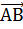 с координатными осями, если
с координатными осями, если 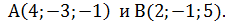
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|