Предел функции на бесконечности. Бесконечно большая функция

Предел функции на бесконечности. Бесконечно большая функция

Рассмотрим функцию 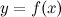, заданную на .

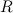Определение

Число 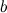называется пределом функции 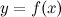на бесконечности или при 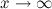, если для любого 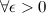существует число 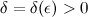такое, что для всех 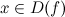из того, что 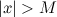, выполняется неравенство .

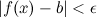Определение

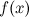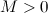Функция называется бесконечно большой в точке , если для любого существует такое 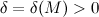, что для любого 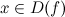, удовлетворяющего неравенству 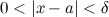, выполняется неравенство: 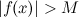. В этом случае пишут: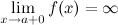

Определение

Функция 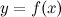называется бесконечно большой при 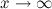, если для любого 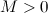существует такое число 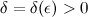такое, что для всех из области определения функции 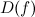, которые удовлетворяют неравенству 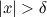, выполняется неравенство :

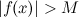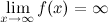
Свойства пределов функции

1° Предел суммы/разности двух функций равен сумме/разности их пределов:

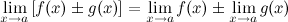
2° Предел произведения двух функций равен произведению их пределов:

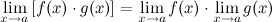
3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

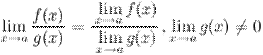
4° Константу можно выносить за знак предела:

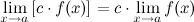
5° Предел степени с натуральным показателем равен степени предела:

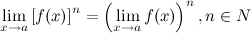
Первый замечательный предел:

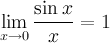
Определение

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Второй замечательный предел:

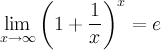
здесь е - число Эйлера.

ХОД РАБОТЫ

Внимательно изучите теоретическую часть практической работы, основные и дополнительные источники и дайте развёрнутые ответы на контрольные вопросы:

1. Дайте определение предела функции.

2. Сформулируйте теорему о пределах суммы, разности, произведения и частного функций

3. Дайте определение одностороннего предела, правого и левого пределов.

4. Сформулируйте определение бесконечно большой и бесконечно малой функции.

5. Какие вы знаете свойства пределов.

6. Первый и второй «замечательные» пределы.

Основные источники:

1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2018.

Дополнительные источники:

2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.

3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.

4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://school-collection.edu.ru/catalog/– Загл. с экрана;

5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: http://window.edu.ru/– Загл. с экрана;

⇐ Предыдущая 12