
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №6.. Тема: «Приложение интеграла к решению физических и геометрических задач». Теоретическая часть.. Формула Ньютона – Лейбница
Практическая работа №6.
Тема: «Приложение интеграла к решению физических и геометрических задач»
Цель: закрепить умения вычислять определѐнные интегралы разными методами,
применять определѐнные интегралы при решении задач физики и геометрии.
Теоретическая часть.
Формула Ньютона – Лейбница
Если функция 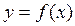 непрерывна на отрезке [a;b] и функция у = F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница
непрерывна на отрезке [a;b] и функция у = F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница
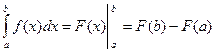 .
.
Вычисление площади плоской фигуры
Найдем площадь S криволинейной трапеции, ограниченной кривой 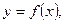 осью
осью 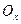 и двумя прямыми
и двумя прямыми 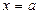 и
и 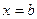 , где
, где 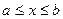 ,
, 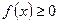 (рис. 1)
(рис. 1)
Так дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой 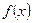 , т. е.
, т. е. 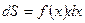 , то, интегрируя это равенство в пределах от a до b, получим
, то, интегрируя это равенство в пределах от a до b, получим
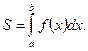
(1)
Если криволинейная трапеция прилегает к оси 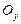 так, что
так, что 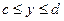 ,
, 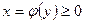 (рис. 2), то дифференциал переменной площади S равен
(рис. 2), то дифференциал переменной площади S равен 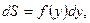 откуда
откуда
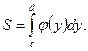
(2)
В том случае, когда криволинейная трапеция, ограниченная кривой 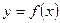 , осью
, осью 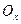 и прямыми x=a и x=b, лежит под осью
и прямыми x=a и x=b, лежит под осью 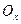 (рис. 3), площадь находится по формуле
(рис. 3), площадь находится по формуле
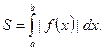
(3)
Если фигура, ограниченная кривой 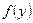 , осью
, осью 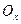 и прямыми x=a и x=b, расположена по обе стороны от оси
и прямыми x=a и x=b, расположена по обе стороны от оси 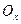 (рис. 4), то
(рис. 4), то
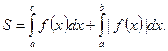
(4)
Пусть, наконец, фигура S ограничена двумя пересекающимися кривыми 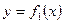 и
и 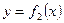 и прямыми x=a и x=b, где
и прямыми x=a и x=b, где 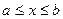 и
и 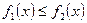 (рис. 5). Тогда ее площадь находится по формуле
(рис. 5). Тогда ее площадь находится по формуле
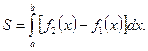
(5)
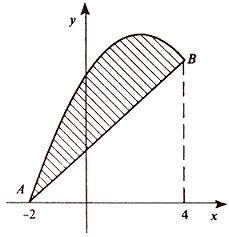
Пример 1. Вычислить площадь фигуры, ограниченной линиями 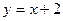 ,
, 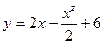 .
.
Решение. Находим точки пересечения заданных линий.
Для этого решаем систему уравнений: 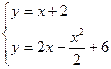
 Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение: 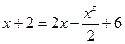 или
или 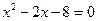 .
.
Находим: x1 = – 2, x2 = 4. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
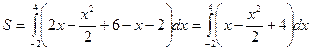 .
.
По формуле Ньютона-Лейбница находим:
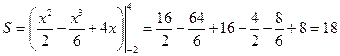 .
.
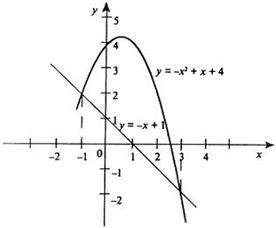 Пример 2. Найти площадь фигуры, ограниченной линиями
Пример 2. Найти площадь фигуры, ограниченной линиями 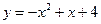 и
и 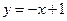 .
.
Решение. Найдем точки пересечения линий 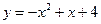 ,
, 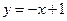 , приравнивая ординаты линий:
, приравнивая ординаты линий: 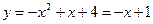 или
или 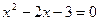 . Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
. Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
По формуле площади фигуры получаем
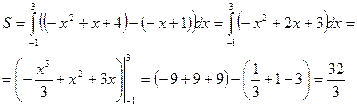
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|