
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Применение производной к исследованию функций».
Стр 1 из 2Следующая ⇒
«Применение производной к исследованию функций».
Выполните задания по образцу (таблица второй столбик)
Задания:
1. Определите критические точки функции: (первые три пункта 1-й таблицы)
а) f(x) = х2 – 6х ;
б) f(x) = 12х – х3.
2. Найдите промежутки монотонности (Возрастание и убывание функции) (первые четыре пункта 1-й таблицы)
а) f(x) = х2 – 2х + 5 ;
б) f(x) = х2 + 12х – 15 .
3. Найти точки экстремума функции: y= 5x3 - 15x - 5.( все пункты 1-й таблицы)
4. Найдите наибольшее и наименьшее значение функции на отрезке:(2-я таблица)
а) f(x) = х3 – 6х2 + 9 [0; 2] ;
СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ ИНТЕРВАЛОВ МОНОТОННОСТИ И ЭКСТРЕМУМОВ
| Этапы | Пример для функции у = 2х3 - Зх2 - 36х + 5 |
| Найти область определения функции и интервалы, на которых функция непрерывна. | Обл. определения: R Функция непрерывна во всей обл. определения |
| Найти производную f'(x). | f'(x)=6x2-6x-36 |
| Найти критические точки, т.е. точки, в которых производная функции равна нулю или не существует. | f'(x)=0, 6x2-6x-36=0, x1=-2, x2=3 |
| В каждом из интервалов, на которые область определения разбивается критическими точками, определить знак производной и характер изменения функции (с помощью достаточных условий монотонности). | 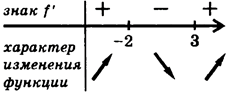
|
| Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума. | x=-2 -точка максимума (xmax=-2) x=3-точка минимума (xmin=3) |
| Записать результат исследования функции: промежутки монотонности и экстремумы. | f(x) возрастает при х 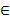 ( ( 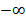 ; -2) и
при х ; -2) и
при х 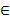 (3; (3; 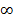 );
f(x) убывает при x );
f(x) убывает при x 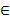 (-2; 3);
xmax=-2, ymax = f(-2) = 49;
xmin=3, ymin = f(3)= -76 (-2; 3);
xmax=-2, ymax = f(-2) = 49;
xmin=3, ymin = f(3)= -76
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|