Задание 2. элементов). Формулы 5 элементов. Аналогии(пропорции) Модью Непера для углов. Аналогии(пропорции) Модью Непера для сторон. B(f1;l1) f1=90-c l1=l2-/\l. C(f2;l2) f2=90-b l2=l1+/\l. K=sinA/sina=sinB/sinb=sinC/sinc. d(склонение)=90-a. tпр=B(в полукр

Задание 2

Прямоугольным сферическим треугольником называется такой сферический треугольник, у которого один из углов равен 90°

Четвертным сферическим треугольником называется такой сферический треугольник, у которого одна из сторон равна 90°.

Косоугольным сферическим треугольником называется такой сферический треугольник, у которого все стороны и углы не равны 90°.

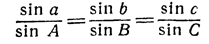
- Теорема синусов

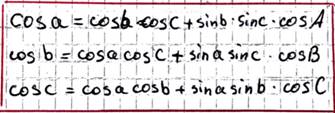
- Теоремы косинусов сторон

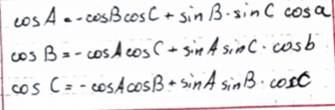
- Теоремы косинусов углов

- Формулы котангенсов(формулы 4-

элементов)

- Формулы 5 элементов

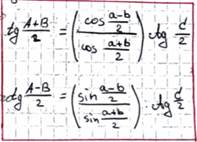
- Аналогии(пропорции) Модью Непера для углов

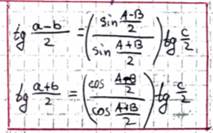
- Аналогии(пропорции) Модью Непера для сторон

Для географических координат:

А=Р_N

B(f1;l1) f1=90-c l1=l2-/\l

C(f2;l2) f2=90-b l2=l1+/\l

Az1=B

Az2=360-C

D=a*60’

K=sinA/sina=sinB/sinb=sinC/sinc

Для астрономических:

f=90-c

d(склонение)=90-a

tпр=B(в полукруговом счете)

h=90-b

A=A(в четвертном счете)

Задание 3

Раздел 1

Раздел 2

Раздел 3

⇐ Предыдущая 12