Хелпикс

Главная

Контакты

Случайная статья



VI. Свойство сложения противоположных чисел.

⇐ ПредыдущаяСтр 2 из 2


VI. Свойство сложения противоположных чисел.

a+(-a)=0, 5+(-5)=0

VII. Свойства деления.

a:1=a

a:a=1

0:a=0

 

 

Вопрос 2. Признаки равенства прямоугольных треугольников.

Признаки равенства прямоугольных треугольников

В двух треугольниках всегда есть один равный элемент – это прямой угол. Когда нужно доказать равенство прямоугольных треугольников, ищут только два равных элемента.

Из первого признака равенства треугольников получаем первый признак равенства прямоугольных треугольников.

Признак I

Если катеты одного прямоугольного треугольника соответственно равны катетам другого треугольника, то такие треугольники равны.

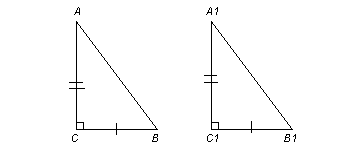
Треугольники равны

«по двум катетам».

 

Из второго признака равенства треугольников получаем второй признак равенства прямоугольных треугольников.

Признак II

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.

Треугольники равны

«по катету и прилежащему острому

углу».

 

 

Признак III («по катету и противолежащему острому углу»)

Если катет и противолежащий ему острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого треугольника, то такие треугольники равны.

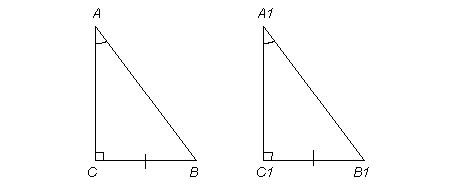Дано: 

, ,

, .

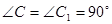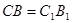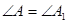Доказать:

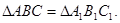
Доказательство:

I) 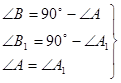 Тогда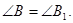

II) Рассмотрим прямоугольные треугольники АВС и А1В1С1.    

1) СВ = С1В1 (по условию).

2) 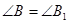 (по доказанному в I).

Тогда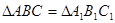  

(по катету и прилежащему острому углу).

Что и требовалось доказать.

 

Признак IV («по гипотенузе и острому углу»)

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны.

Дано: 

,  

,

, .

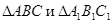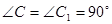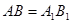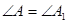Доказать:

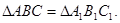
Доказательство:

I) 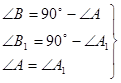 Тогда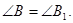

II) Рассмотрим треугольники АВС и А1В1С1.                                         

1) АВ = А1В1 (по условию).

2) 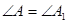 (по условию).

3) 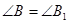 (по доказанному в I).

Тогда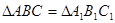  

(по стороне и 2 прилежащим к ней углам).

Что и требовалось доказать.

Признак V («по гипотенузе и катету»)

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Дано: 

,  

,

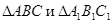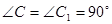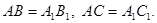
Доказать:

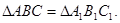
Доказательство:

I) Мысленно наложим 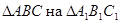 так, чтобы.  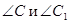совпали. Тогда АС  и А1С1 совпадут, значит, совпадут вершины А и А1.

II) Мы не уверены, что совпадут ли АВ с А1В1. Предположим, что АВ не совпадет с А1В1, а совпадет с А1В2.

III) А1В2 = АВ (по предположению)

А1В1 = АВ (по условию)

Отсюда А1В2 = А1В1, тогда 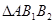- равнобедренный (по определению равнобедренного треугольника). Значит, по свойству равнобедренного треугольника .

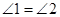Получили противоречие, т.к. 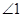- тупой, а 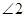- острый.

Значит, наше предположение неверно.

Тогда АВ совпадет с А1В1, т.е. совпадут вершины В и В1.

Треугольники полностью совпали, значит,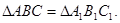

Что и требовалось доказать.

 

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.