
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Билет 1. I. Переместительное.. II. Сочетательное.. III. Распределительное.. IV. Свойство 1. V. Свойство 0
Стр 1 из 2Следующая ⇒
Билет 1
Вопрос 1. Числа. Свойства действий над числами.
| N – натуральные числа.N={1,2,3,4,5,…} Натуральными числами называются числа, употребляемые при счете предметов. Выполнимы операции: +,*. Не всегда выполнимы: -, : Пример: 5-3=2, 3*12=45, | Z –целые числа.Z={…,-3,-2,-1,0,1,2,3,…} Целыми числами называются натуральные числа, им противоположные и 0. Выполнимы операции: +,*,-. Не всегда выполнима :. Пример: -3+5=2 |
Q – рациональные числа.
Q={  }, mÎZ, nÎN
Рациональными числами называются числа, которые можно представить в виде дроби, у которой числитель – Z, а знаменатель – N.
Выполнимы операции: +,-,*,:
Примеры: }, mÎZ, nÎN
Рациональными числами называются числа, которые можно представить в виде дроби, у которой числитель – Z, а знаменатель – N.
Выполнимы операции: +,-,*,:
Примеры: 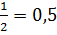 ; ; 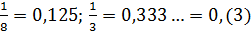 — бесконечная периодическая дробь.
Вывод:рациональные числа всегда можно представить в виде конечной десятичной дроби или бесконечной периодической дроби. — бесконечная периодическая дробь.
Вывод:рациональные числа всегда можно представить в виде конечной десятичной дроби или бесконечной периодической дроби.
| · R – действительные числа.
Действительными числами называются числа рациональные и иррациональные.
Иррациональные числа – это бесконечные непериодические десятичные дроби.
Примеры:
p=3,14159265…; 0,123456789…
e»2,718281…
ü 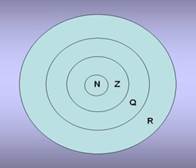 Круги Эйлера Круги Эйлера
|
Свойства действий над числами.
1. Название
2. Формула.
3. Формулировка.
4. Пример.
I. Переместительное.
a+b=b+a, 5+13=13+5
a∙b=b∙a, 5∙13=13∙5.
II. Сочетательное.
a+b+c=a+(b+c)= (a+b)+c, 5+13+7=5+(13+7)=25;
a∙b∙c=(a∙b)∙c=a∙(b∙c), 13∙2∙5=13∙(2∙5)=130
III. Распределительное.
(a+b)∙c=ac+bc,
(a-b)∙c=ac-bc.
IV. Свойство 1
a∙1=1∙a=a
13∙1=1∙13=13
V. Свойство 0
a+0=0+a=a, 13+0=0+13=13
a∙0=0∙a=0, 13∙0=0∙13=0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|