Билет № 7. а+в)(с+d)= ac+bc+ad+bd.. а+в)(с+d)= ac+bc+ad+bd.

Стр 1 из 2Следующая ⇒

Билет № 7

1. Умножение многочлена на многочлен. Разложение многочлена на множители способом группировки.

Умножение многочлена на многочлен. (а+в)(с+d) =ac+bc+ad+bd.

· Обозначим многочлен а+в=х, получим х(с+d).

· Применим правило умножения одночлена на многочлен: хс+xd.

· Заменим х наа+в и получим: (a+b)c+(a+b)d.

· По правилу умножения одночлена на многочлен: ac+bc+ad+bd.

(а+в)(с+d)= ac+bc+ad+bd.

Правило:Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена поочерёдно на каждый член другого многочлена и полученные произведения сложить.

Пример: (5x+1)(3x-4)=5x*3x+5x(-4)+3x*1 - 4=15x²- 20x+3x -4=15x²-17x-4.

Выясним геометрический смысл формулы (а+в)(с+d)= ac+bc+ad+bd

для положительных а, в, с. а>0, b>0, c>0,d>0.

axd

axc

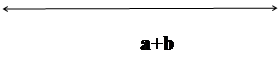
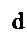
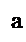
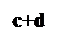
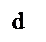
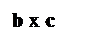
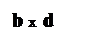
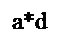
Геометрический смысл: чтобы найти S прямоугольника со сторонами а+b и с+d, нужно найти сумму площадей прямоугольников со сторонами aи d, a и c, b и d, b и c.

(а+в)(с+d)= ac+bc+ad+bd.

Разложение многочлена на множители способом группировки.

При разложении многочлена на множители применяют метод группировки. Члены многочлена объединяют в группы или группируют. После этого в каждой группе выносят общий множитель за скобки. Если в скобках остаётся одинаковый многочлен, то его так же выносят за скобки.

Примеры:

1. 2a²+6a+ab+3b=(2a²+6a)+(ab+3b)=2a(a+3)+b(a+3)=(a+3)(2a+b)

2. 2a²+6a+ab+3b=(2a²+ab)+(6a+3b)=a(2a+b)+3(2a+b)=(2a+b)(a+3)

3. 2a²+6a+ab+3b=(2a²+3b)+(6a+ab)- неудачная группировка.

II.

1. xy-6+3x-2y=(xy+3x)-(6+2y)=x(y+3)-2(3+y)=(3+y)(x-2)

2. xy-6+3x-2y=(xy-2y)+(3x-6)=y(x-2)+3(x-2)= (x-2)(y+3)

III. Решение уравнений.

1. x³ – 2x²+3x – 6=0

(x³-2x²)+ (3x-6)=0

x²(x-2)+3(x-2)=0

(x-2)(x²+3)=0

x-2=0 x²+3=0

x=2 корней нет

Ответ:x=2.

2. x²-7x+12=0

x²-4x-3x+12=0

(x²-4x)- (3x-12)=0

x(x-4) – 3(x-4)=0

(x-4)(x-3)=0

x-4=0 x-3=0

x=4 x=3

Ответ: x=4; x=3.

12 Следующая ⇒