I. Прямая пропорциональность, её график и свойства.

Билет № 13

I. Прямая пропорциональность, её график и свойства.

Определение. Функция вида y = kx называется прямой пропорциональностью, где k – число, а х и у – переменные (является частным случаем линейной функции y = kx +m, при m =0).

k- коэффициент пропорциональности. k= .

Графиком прямой пропорциональности является прямая, проходящая через начало координат.

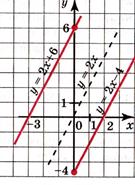Пример: y=2x.

x	2
y	4

Прямая, являющаяся графиком линейной функции y=kx+m, параллельна прямой, являющейся графиком прямой пропорциональности y=kx.

Свойства функции.


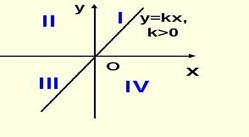
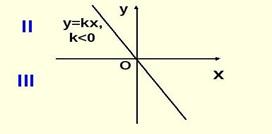
y = kx (k > 0)	y = kx (k <0)
D(y)=R	D(y)=R
E(y)=R	E(y)=R
с OY: (0;0) с OX : (0;0)	с OY: (0;0) с OX : (0;0)
нули:x=0	нули:x=0
у >0 при х ϵ (0;∞) или при х >0 у<0 при х ϵ (- ∞; 0) или при x<0	5) у >0 при х ϵ (-∞; 0) или при х< 0 у<0 при х ϵ (0;∞) или при х >0
y возрастает на D	y убывает на D
Нечётная у(-х) = -у (х), график функции симметричен относительно начала координат.	Нечётная у(-х) = -у (х), график функции симметричен относительно начала координат.
непрерывна на D	непрерывна на D
не ограничена на D	не ограничена на D
наибольшего и наименьшего значений нет	наибольшего и наименьшего значений нет

II. Частные случаи линейной функции.

1. y=x – уравнение биссектрисы I и III координатных углов.	Привести пример
2. y=-x -уравнение биссектрисы II и IV координатных углов.	Привести пример
2. y= m прямая ll Ox, проходящая через точку с координатами (0;m). y=2 (0;2) y= -3 (0;-3) y=0 (0;0)-уравнение оси абсцисс	Привести пример

12 Следующая ⇒