
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пусть функции и имеют в точке пределы и . Тогда функция всегда имеет в точке предел равный . Нет.
2)Пусть функции и имеют в точке пределы и . Тогда функция всегда имеет в точке предел равный . Нет.
3)Пусть функции и , определенные в некоторой окрестности точки таковы, что и функции и имеют в точке предел равный , тогда справедливо неравенство . Нет.
4)Функция не может иметь двух различных пределов в данной точке.
Да.
4.Верны ли утверждения?
1)Функция ограничена на интервале . Да.
2)Функция ограничена в области . Да.
3)Функция не ограничена сверху в интервале , где . Нет.
4)Колебание функции на интервале не определено. Нет.
5.Верны ли утверждения?
1) . Да.
2) . Да.
3) . Нет.
4) . Да.
5) . Нет.
6) . Да.
7) . Нет.
6.Верны ли утверждения?
1) . Нет.
2) . Нет.
3) . Нет.
4) . Да.
5) . Да.
6) . Да.
7.Пусть 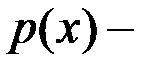 многочлен степени
многочлен степени 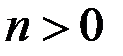 со старшим коэффициентом
со старшим коэффициентом 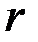 , а
, а 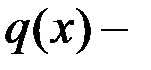 многочлен степени
многочлен степени 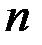 со старшим коэффициентом
со старшим коэффициентом 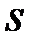 . Верны ли утверждения?
. Верны ли утверждения?
1) . Нет.
2) . Да.
3) . Нет.
8.Пусть 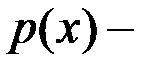 многочлен степени
многочлен степени 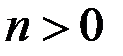 , а
, а 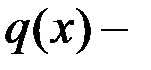 многочлен степени
многочлен степени 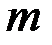 . Верны ли утверждения если
. Верны ли утверждения если 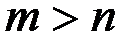 ?
?
1) . Нет.
2) . Нет.
3) . Да.
9.Пусть 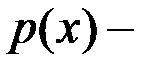 многочлен степени
многочлен степени 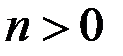 , а
, а 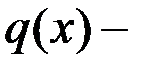 многочлен степени
многочлен степени 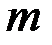 (не тождественно равный нулю). Верны ли утверждения если
(не тождественно равный нулю). Верны ли утверждения если 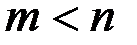 и
и 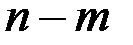 -четно?
-четно?
1) . Нет.
2) . Да.
3) . Нет.
10.Пусть 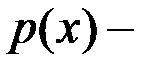 многочлен степени
многочлен степени 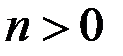 , а
, а 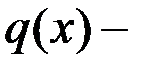 многочлен степени
многочлен степени 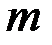 (не тождественно равный нулю). Если
(не тождественно равный нулю). Если 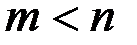 и
и 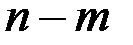 -нечетно, то верны ли утверждения?
-нечетно, то верны ли утверждения?
1) . Да.
2) . Да.
3) . Да.
11.Пусть 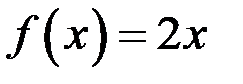 ,
, 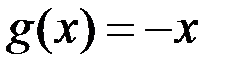 .Верны ли утверждения?
.Верны ли утверждения?
1) . Да.
2) . Да.
3) . Да.
12.Пусть , .Верны ли утверждения?
1) . Да.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|