Предел функции.. Часть 1. Предлагаемые задачи, состоят из нескольких родственных друг другу вопросов. На каждый из вопросов можно дать один из двух ответов: «Да» или «Нет».. Если , то для любого , такое, что для таких, что следует, что .

3. Предел функции.

Часть 1. Предлагаемые задачи, состоят из нескольких родственных друг другу вопросов. На каждый из вопросов можно дать один из двух ответов: «Да» или «Нет».

1.Верны ли утверждения?

1)Если , то для любого , такое, что для таких, что следует, что . Нет.

2)Если , то для любого , такое, что для всех таких, что следует, что . Нет.

3) Если , то для любого , такое, что для всех таких, что следует, что . Да.

4) Если , то для любого , такое, что для всех таких, что следует, что . Да.

5)Если 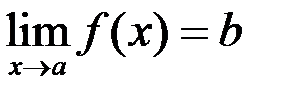, то функция 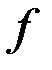определена в некоторой окрестности точки 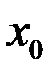, кроме, возможно самой точки 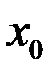, где она может быть не определена. Да.

2.Верны ли утверждения?

1)Если в точке правый и левый пределы функции равны, то в точке существует предел этой функции, равный указанным односторонним пределам. Да.

2)Если в точке предел функции существует, то в этой точке может не существовать, либо правый, либо левый пределы функции. Нет.

3)Если в точке предел функции существует, то в этой точке правый и левый пределы функции могут быть не равны пределу функции в точке . Нет.

4)Если в точке правый и левый пределы функции совпадают, то обязательно существует предел функции в этой точке. Да.

3.Верны ли утверждения?

1)Пусть функции и имеют в точке пределы и . Тогда функция всегда имеет в точке предел равный . Да.

12 3 4 5 6 Следующая ⇒