
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Домашнее задание №2 «СЛУЧАЙНЫЕ ПРОЦЕССЫ»
Домашнее задание №2 «СЛУЧАЙНЫЕ ПРОЦЕССЫ»
Задача 1.
Моделирование гауссовского процесса с данной автоковариационной функцией
На отрезке 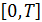 с шагом
с шагом 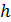 смоделируйте
смоделируйте 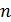 траекторий гауссовского процесса с заданным математическим ожиданием
траекторий гауссовского процесса с заданным математическим ожиданием 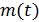 и заданной автоковариационной функцией
и заданной автоковариационной функцией 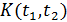 . Выведите на печать две-три траектории.
. Выведите на печать две-три траектории.
Выберите несколько пар сечений построенного процесса (для далеких значений 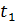 и
и 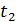 , для близких, для соседних). Постройте для выбранных пар сечений диаграммы рассеяния, вычислите выборочные коэффициенты корреляции, постройте 95% доверительные интервалы и сравните с теоретическими значениями соответствующих коэффициентов корреляции.
, для близких, для соседних). Постройте для выбранных пар сечений диаграммы рассеяния, вычислите выборочные коэффициенты корреляции, постройте 95% доверительные интервалы и сравните с теоретическими значениями соответствующих коэффициентов корреляции.
Сформулируйте выводы.
Алгоритм моделирования траекторий
1. Находим размерность 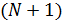 случайного вектора
случайного вектора 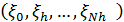 ,
, 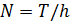 .
.
2. Вычисляем вектор математических ожиданий 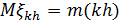 и матрицу ковариаций
и матрицу ковариаций 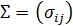 , и
, и 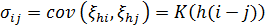 .
.
3. Генерируем с помощью встроенного датчика случайных чисел базовую последовательность независимых стандартных гауссовских случайных величин
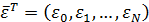
4. Находим квадратный корень Холецкого из матрицы 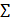 , то есть такую нижнетреугольную матрицу
, то есть такую нижнетреугольную матрицу 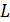 , что
, что 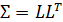 . Тогда, как было доказано на лекции, матрица
. Тогда, как было доказано на лекции, матрица 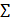 будет ковариационной для центрированной последовательности
будет ковариационной для центрированной последовательности 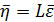 .
.
5. Последний шаг- добавляем нужное математическое ожидание: 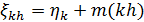 .
.
Замечание. В среде Mathcad имеется встроенная функция, вычисляюшая нижнетреугольную матрицу Холецкого:
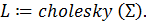
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|