
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рассмотрим основные способы решения показательных уравнений на примерах.
Рассмотрим основные способы решения показательных уравнений на примерах.
Способ 1. Приведение обеих частей уравнения
к общему основанию
Примеры:
1. 9x = 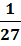
32x = 3-3;
x = -  .
.
Ответ: х =-  .
.
2. 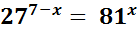
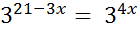 ;
;
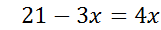 ;
;
x = 3
Ответ: x = 3.
3. 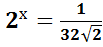
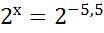 ;
;
х=  Ответ: х=
Ответ: х= 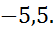
4. (  )x ∙ (
)x ∙ (  )x =
)x = 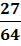
По свойству степени: ( 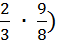 x =
x = 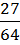 ;
;
(  x = (
x = (  )3 ;
)3 ;
х= 3.
Ответ: х = 3.
5. 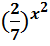 = (
= (  )4-5x
)4-5x
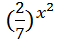 = (
= (  )-4+5x;
)-4+5x;
 x2 = -4 + 5x;
x2 = -4 + 5x;
x2 - 5x + 4 = 0;
x1 =4; x2 =1.
Ответ: x1 = 4; x2 = 1.
Способ 2. Вынесение общего множителя за скобку
Примеры:
1. 6x+1 + 356x-1 = 71
6x-1(62+35) = 71;
6x-1 = 1;
6x-1 = 60;
x = 1.
Ответ: x = 1.
2. 7∙ 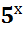 -
- 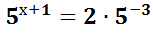
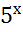 ∙(7-5) =
∙(7-5) = 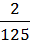
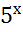 ∙ 2 =
∙ 2 = 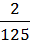
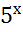 =
= 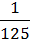
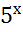 =
= 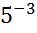 ;
; 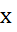 = -3.
= -3.
Ответ: x = -3.
3. 2x + 5 ∙ 2x+1 + 7 ∙ 2x+2 = 312
Вынося в левой части уравнения за скобки общий множитель 2x, получим:
2x ∙ (1+5 ∙ 21+7 ∙ 22) = 312;
2x ∙ 39 = 312;
2x = 8;
2x = 23;
х = 3.
Ответ: х = 3.
4. 3x - 2 ∙ 3x-2 = 63
3x-2 ∙ (32-2) = 63;
3x-2 ∙ 7 = 63;
3x-2 = 9;
3x-2 = 32;
x-2 = 2;
x = 4.
Ответ: x = 4.
5. 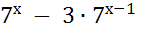 +
+ 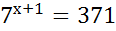
Наименьшим показателем степени является х-1; поэтому вынесем за скобки 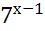 :
:
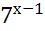 (
( 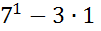 +
+ 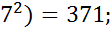
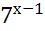 (
( 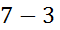 +
+ 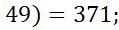
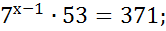
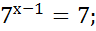
х - 1= 1;
х = 2.
Ответ: x = 2.
Способ 3. Приведение показательного уравнения
к квадратному уравнению
1. 72x - 8 ∙ 7x + 7 = 0
Данное уравнение имеет вид Aa2 x+ Bax + C = 0.
Пусть 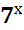 = у, тогда 72x = у2 и для определения y получим квадратное уравнение: y2 - 8y + 7 = 0;
= у, тогда 72x = у2 и для определения y получим квадратное уравнение: y2 - 8y + 7 = 0;
y1 = 7; y2 = 1.
Осуществляя обратную подстановку, получим два уравнения, из которых получим два корня исходного уравнения:
1) 7x = 7; 7x = 71; x = 1;
2) 7x = 1; 7x = 70; x = 0;
Ответ: x1 = 1; x2 = 0.
2. 5∙52x - 6 ∙ 5x + 1 = 0
Пусть: 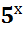 = у, тогда получим квадратное уравнение вида
= у, тогда получим квадратное уравнение вида
5у2 - 6у + 1у = 0:
D=16; у1= 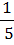 , у2= 1.
, у2= 1.
Осуществляем обратную подстановку:
так как у1 = 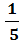 , то
, то 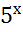 =
= 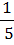 , х = -1;
, х = -1;
у2 = 1, то 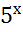 = 1 , х = 0;
= 1 , х = 0;
Ответ: x1 = -1; x2 =0.
3. 22+x - 22-x = 15;
22 ∙ 2x - 22 ∙ 2-x = 15;
Получили уравнение вида Aax + Ba-x + C = 0.
Используя подстановку 2x = y и 2-x 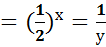 , переходим к уравнению 4y -
, переходим к уравнению 4y -  = 15 или 4y2 - 15y - 4 = 0.
= 15 или 4y2 - 15y - 4 = 0.
Находим корни уравнения: y1 = 4; y2 = -  .
.
Осуществляем обратную подстановку:
1) 2x = 4; 2x = 22; x = 2;
2) 2x = -  - корней нет, так как 2x>0, x
- корней нет, так как 2x>0, x 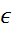 R.
R.
Ответ: x = 2.
4. 4x + 6x = 2 ∙ 32x
22x + 2x ∙ 3x - 2 ∙ 32x = 0.
Разделим обе части последнего уравнения почленно на 32x:
получим уравнение 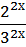 +
+ 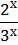 -2 = 0.
-2 = 0.
Преобразуя, в соответствии со свойством степеней, получим квадратное уравнение вида (  )2x + (
)2x + (  )x - 2 = 0.
)x - 2 = 0.
Пусть (  )x = y и (
)x = y и (  )2x = y2;
)2x = y2;
решая квадратное уравнение y2+y - 2 = 0, найдем его корни y1 = 1; y2 = -2.
Осуществляем обратную подстановку и находим корни исходного уравнения:
1) (  )x = 1; (
)x = 1; (  )x = (
)x = (  )0; x = 0.
)0; x = 0.
2) (  )x = -2 – корней нет.
)x = -2 – корней нет.
Ответ: x = 0
5. = 0.
Первый член уравнения можно представить в виде
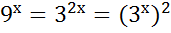 .
.
Тогда исходное уравнение принимает вид
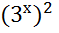 –
– 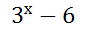 = 0;
= 0;
Обозначим: 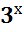 = с, тогда
= с, тогда 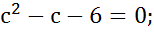
с1 = 3, с2 = 1.
Второй корень смысла не имеет, так как показательная функция всегда положительна.
Итак, 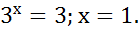
Ответ: x = 1.
ДОМАШНЕЕ ЗАДАНИЕ
1. Представленный материал изучить, рассмотреть решения всех типовых примеров и внести весь изученный материал в конспект по математике.
2. Уметь ответить на контрольные вопросы.
3. Решить представленные ниже три показательных уравнения с пояснением способа решения.
КОНТРЛЬНЫЕ ВОПРОСЫ
1. Перечислите свойства показательной функции.
2. Через какую точку проходят графики всех показательных функций вида y=ax?
3. Какое уравнение называется показательным?
4. Сформулируйте правило решения простейших показательных уравнений.
5. При каких bпоказательное уравнение a x= b имеет корень?
6. Сколько корней имеет уравнение ax=b?
7. Как решать уравнение вида af(x)=ag(x)?
Решите уравнения:
ü 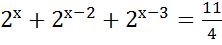 .
ü .
ü 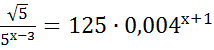 .
ü .
ü 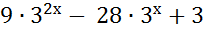 =0. =0.
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|