Хелпикс

Главная

Контакты

Случайная статья



ТЕМА. Способы решения. показательных уравнений. Понятие показательного уравнения. Виды показательных уравнений и способы их решений. ДОМАШНЕЕ ЗАДАНИЕ

Стр 1 из 2Следующая ⇒


ТЕМА. Способы решения

показательных уравнений

 

Вопросы темы:

1. Понятие показательного уравнения

2. Виды показательных уравнений и способы их решений

3. ДОМАШНЕЕ ЗАДАНИЕ

 

Вопрос 1. Понятие показательного уравнения

1. Уравнение – это равенство, содержащее неизвестную величину, значение которой нужно найти.

2. Корень уравнения – это значение неизвестной величины, при котором равенство не теряет смысла.

3. Решить уравнение – значит найти все его корни или доказать, что корней нет.

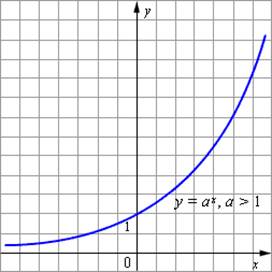
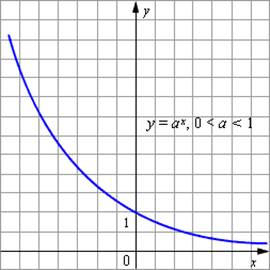
4. Функция, заданная формулой у = ах (где а > 0, а≠ 1), называется показательной функцией с основанием а.

D(y) = R (область определения – множество всех действительных чисел).

E(y) = R+ (область значений – все положительные числа).

при а > 1, функция возрастает

при 0 < а < 1, функция убывает

Определение 1. Показательными уравнениями называются уравнения, содержащие неизвестную величину в показателе степени.

Например, уравнение

,

 

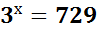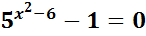
Определение 2. Простейшим показательным уравнением называется уравнение вида: ax = b.

 

Пусть: - основание a > 0 , а≠1. Так как функция y = ax строго монотонна, то каждое свое значение она принимает ровно один раз. Это означает, что уравнение ax = b при b > 0 имеет единственный корень х = 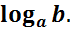- еслиb ≤ 0, то уравнение ax = b корней не имеет, так как ax 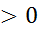 . - если число b записано в виде ax = ac, то оно имеет один корень x = c.   При решении показательных уравнений необходимо помнить, что решение любого показательного уравнения сводится к решению “простейших” показательных уравнений.
 
Вопрос 2. Виды показательных уравнений и способы их решений

12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.