Тригонометрическое уравнение — уравнение, содержащее неизвестное под знаком тригонометрической функции.

Стр 1 из 2Следующая ⇒

Глава: Тригонометрические уравнения

1. Арккосинус и уравнение cos x = a

Теория:

Тригонометрическое уравнение — уравнение, содержащее неизвестное под знаком тригонометрической функции.

Уравнения видаsinx=a,cosx=a,tgx=a,ctgx=aназываются простейшими тригонометрическими уравнениями.

Уравнение cosx=a

Если |a|>1, то уравнение cosx=a не имеет корней.

Например, уравнение cosx=−1,5 не имеет корней.

Если |a|≤1, то корни уравнения выражаются формулой x = ±a rccos a+2πk, k∈Z.

Что же такое arccos a? Арккосинус в переводе с латинского означает «дуга и косинус». Это обратная функция.

Если |a|≤1, то arccos a (арккосинус а) — это такое число из отрезка [0;π], косинус которого равен а.

Говоря иначе:

Arccos a= x ⇒ если cos x = a, |a|≤1,x∈[0;π].

Пример:

найти arccos.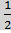

Выражение arccos 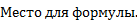показывает, что косинус угла x равен

(cos x= ).

Далее просто находим точку этого косинуса в таблице тригонометрических значений

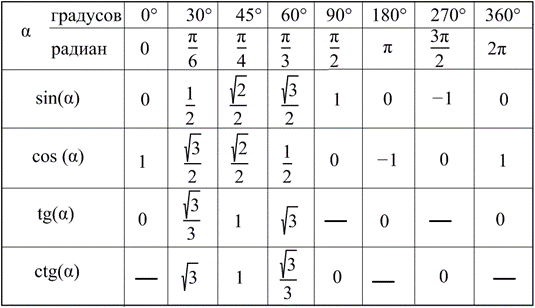
Значит, arccos =.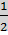

Обрати внимание!

Если cos π/3= , то arccos =π/3.

В первом случае по таблице тригонометрических значений определяем значение косинуса, а во втором — наоборот, по значению косинуса находим угол. Движение в обратную сторону. Это и есть арккосинус.

Теорема. Для любого a∈[−1;1] выполняется равенство arccosa+arccos(−a)=π.

Частные случаи:

1. cosx=0⇒x=π/2+πk,k∈Z;

2. cosx=1⇒x=2πk,k∈Z;

3. cosx=−1⇒x=π+2πk,k∈Z.

Пример:

решить уравнение cosx=2/5.

Используем формулу x = ± arccos a+2πk,k∈Z и

получаем ответ x= ± arccos 2/5+2πk,k∈Z.

2,3 Уравнение sin x = a, tg x = a,

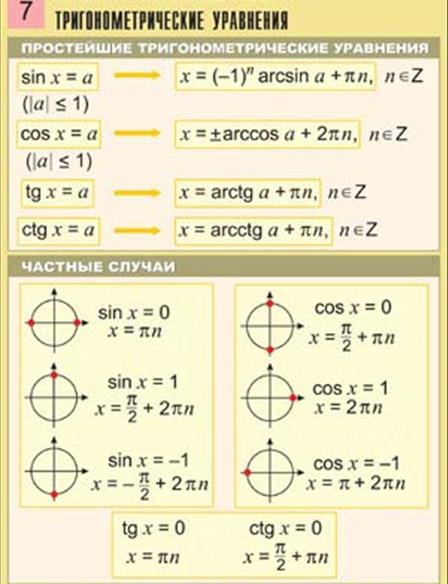
Аналогично изучаются и решаются уравнения sin x = a, tg x = a, только число а подставляется в свои соответствующие формулы(см . ниже)

12 Следующая ⇒