Практическая работа № 6. Изучение минимизации логических функций с использованием законов и тождеств алгебры логики. Порядок выполнения. Теоретическая часть

Практическая работа № 6

Изучение минимизации логических функций с использованием законов и тождеств алгебры логики

Цель:Изучить основные и дополнительные законы алгебры логики; ознакомиться с понятием логической функции от n аргументов; научиться составлять таблицы истинности для логических функций от n аргументов; используя таблицы истинности

Порядок выполнения

Изучить теоретическую часть
Выполнить практическое задание
Ответить на контрольные вопросы
Оформить отчет по проделанной работе

Теоретическая часть

Алгебра высказываний (алгебра логики) является моделью класса моделей (М, +,•, 0, 1).Каждая модель этого классаназываетсябулевой алгеброй.Алгебра логики строится на множестве М = {И, Л}, т.е. М – множество истинных и ложных высказываний. Операции "+" соответствует дизъюнкция, а "•" – конъюнкция.

Имеем систему ({И, Л}, Ú, Ù, И, Л),но, поскольку эта система является булевой алгеброй,онадолжна удовлетворять аксиомам 1-8. Аксиомы 1-8, отражающие конкретную природу элементов множества-носителя М и смысл операций "+" и "•",фактическиявляются законами алгебры логики ивыглядят следующим образом:

- аксиомы коммутативности

- аксиомы дистрибутивности

- нейтральный элемент относительно конъюнкции

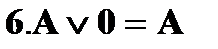- нейтральный элемент относительно дизъюнкции

- закон исключенного третьего

- аксиомы ассоциативности

12 Следующая ⇒