
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Параметрическое программирование
Параметрическое программирование
Переменные
#0 - всегда нуль. Этой переменной нельзя присвоить никакого значения.
#1 - #33 – Локальные переменные. При отключении питания обнуляются.
#100 - #199 – Общие переменные. При отключении питания обнуляются.
#500 - #999 – Общие переменные. При отключении питания данные сохраняются.
Диапазон значений переменных:
от -1047 до -10-29
от +10-29 до +1047
Примеры:
#1=123
X#1
Z[#1/2]
Ограничения использования:
Нельзя использовать переменные в качестве номера программы (O#10),
в качестве номера кадра (N#20) и после наклонной черты в начале кадра (/#30).
Действия с переменными:
4 арифметических действия + - * /
SIN[…](синус), COS[…],TAN[…], ASIN[…](арксинус), ACOS[…], ATAN[…]
SQRT[…](квадратный корень), ABS[…](модуль числа), ROUND[…](округление),
FIX[…](округление в меньшую сторону), FUP[…](округление в большую сторону),
LN[…], EXP[…],
OR(логическое ИЛИ), XOR(исключающее ИЛИ), AND(логическое И).
Операторы сравнения:
GT больше
LT меньше
EQ равно
NE не равно
GE больше или равно
LE меньше или равно
Переходы и повторы:
GOTO100 – Переход на кадр N100, безусловный
IF [#1GT10] GOTO100 – Переход на кадр N100, если #1>10
IF [#1GT10] THEN #2=20 – Присвоение #2=20, если #1>10
WHILE [#1GT10] DO1
#1=#1+1
G0 X#1
END1
 Пример параметрической программы:
Пример параметрической программы:
Токарная обработка
Напишем чистовую обработку такого валика, размеры которого сведены в таблицу:
| Деталь | D1 | L | R1 | R2 |
| 000.00.00 | ||||
| 000.00.00-01 | ||||
| 000.00.00-02 | ||||
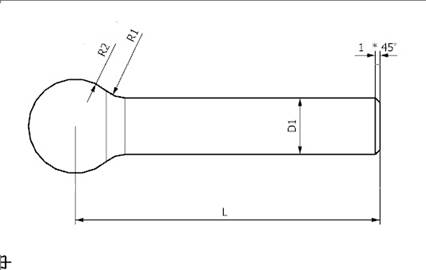 000.00.00-03 000.00.00-03
|
В начале программы введем переменные:
O0001(PRIMER 1)
N10 #501=12(D1)
N40 #504=65(L)
N50 #505=5(R1)
 N60 #506=10(R2)
N60 #506=10(R2)
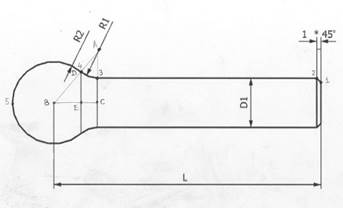
Чтобы выполнить чистовую обработку, нам необходимо знать координаты всех опорных точек. Обозначим эти точки цифрами и буквами.
1 (#1;#2) (#1 – координата точки 1 по оси X, #2 - по оси Z)
2 (#3;#4)
3 (#5;#6)
4 (#7;#8)
5 (#9;#10)
A (#11;#12)
B (#13;#14)
Теперь присвоим этим переменным известные значения:
Точка 1 – начало траектории, ее координата по X будет равна значению диаметра D1 уменьшенного на двойную величину фаски 1*45°, т.е. D1-2. Значение D1 хранится в переменной #501, тогда получим наше первое вычисление
N70 #1=#501-2
Координата точки 1 по Z равна нулю,
N80 #2=0
Далее, для точки 2:
N90 #3=#501
N100 #4=-1
Для точки 3 мы пока знаем только координату по X:
N110 #5=#501
Для точки 4 неизвестны пока обе координаты, пропустим ее, и укажем оставшиеся известные значения:
N120 #9=0
N130 #10=-#504-#506
N140 #11=#501+#505*2
Здесь, по правилам математики, система сначала выполнит умножение (#505*2), а затем сложение
N150 #13=0
N160 #14=-#504
Выделим известные координаты наших точек:
1 (#1;#2)
2 (#3;#4)
3 (#5;#6)
4 (#7;#8)
5 (#9;#10)
A (#11;#12)
B (#13;#14)
Теперь определим оставшиеся 4 неизвестные пока координаты:
Чтобы найти координату точки 3 по Z, нужно найти величину отрезка BC.
Условие касательного сопряжения дуг определяет, что прямая AB проходит через точку 4.
Рассмотрим треугольник ABC:
Он прямоугольный, по теореме Пифагора, AB2=BC2+AC2
Тогда, BC2= AB2-AC2
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|