Сложение. Вычитание. Умножение. Обратное преобразование результатов. II. Практическая часть. Задание 1.

⇐ ПредыдущаяСтр 2 из 2

Сложение

Шаг №1. Вычислить: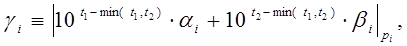

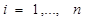
Шаг №2.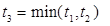

Вычитание

Шаг №1. Вычислить: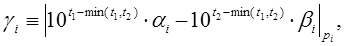

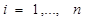
Шаг №2.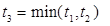

Умножение

Шаг №1. Вычислить: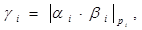

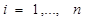
Шаг №2.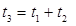

4. Обратное преобразование результатов

Пусть в результате вычислений по правилам из пункта 2 получилось число

A₃=[ (y₁,y₂,…,y_n), t) ]

Шаг №1. Вычислить значения
K= [y₁ mod p₁, y₂ mod p₂, …, y_n mod p_n]

Шаг №2. Преобразовать К в позиционную систему счисления

Вариант 1. На основе китайской теореме об остатках.

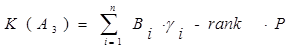, (7)

где

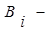ортогональные базисы,

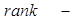ранг, наибольшее положительное целое число,
такое, что .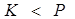

Ортогональные базисы 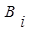являются константами для МСС с заданными модулями и определяются по формулам:

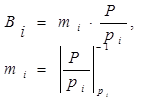(8)

Ранг можем найти как частное от деления суммы на Р.

Вариант 2. На основе смешанной системы счисления

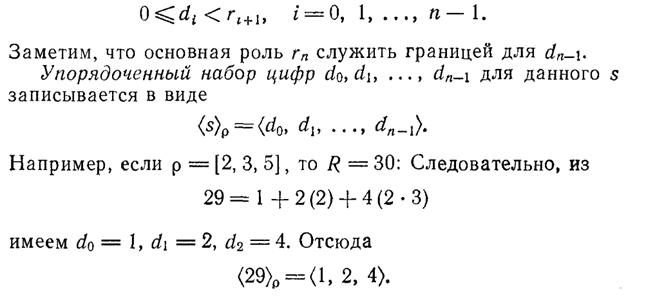
Шаг №3

С учётом пункта 2 определить знак К и вычислить K*10^t, которая будет являться результатом.

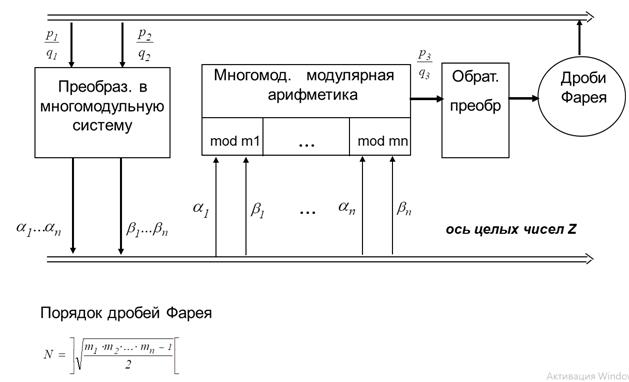
Рисунок 1. Вычисления с исключением ошибок округления по нескольким модулям

II. Практическая часть

Задание 1.

1. Разработать программу для реализации вычислений с исключением ошибок округления по нескольким модулям по схеме приведенной в теоретической части, с 3 арифметическими операциями. Реализовать прямое и обратное преобразование чисел вида (1) в позиционную систему счисления внутри класса. Проверить работу этой программы на примере выполнения арифметических операций с числами вида (1)

Задание 2.

2. Решить задачу последовательно на одном компьютере по нескольким модулям.

Вариант 1.

Найти сумму N случайных положительных дробей у которых степень знаменателя изменяется в некотором диапазоне и числитель случайное число, принадлежащее некоторому диапазону. Для этой задачи определить какой максимально возможный по величине числитель и знаменатель дроби возможен и исходя из этой дроби и выбрать модули

Вариант 2.

Найти скалярное произведение двух векторов с N координатами, каждая из которых положительная случайная дробь у которых степень знаменателя изменяется в некотором диапазоне и числитель случайное число, принадлежащее некоторому диапазону. Для этой задачи определить какой максимально возможный по величине числитель и знаменатель дроби возможен и исходя из этой дроби и выбрать модули

III. Литература

1. Грегори Р., Кришнамурти Е. Безошибочные вычисления. Методы и приложения: Пер. с англ. – М.: Мир,1998 – 208 с., ил.

2. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Учебное пособие. – 2-е изд., доп. – М.: Издательство МЭИ, 2003. – 596 с., ил.

⇐ Предыдущая 12