Интегрирование по частям

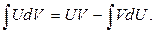    Метод интегрирования по частям заключается в следующем:

1. Подынтегральную функцию исходного интеграла рассматриваем как произведение функции  и дифференциала некоторой функции .

2. За дифференциал  мы должны выбрать выражение, для которого сможем найти  первообразную.

3. После этого применяем формулу (*). Применять формулу имеет смысл в том случае, когда интеграл  окажется проще исходного или подобен ему.

4. Для получения окончательного результата иногда требуется применить метод последовательно несколько раз.

ПРИМЕР:

    Методом интегрирования по частям вычисляются интегралы следующих типов:

1. Интегралы вида , ,  где  - многочлен n-ой степени от х, a≠0, b≠0 – действительные числа.

Чтобы вычислить эти интегралы, надо применить метод интегрирования по частям  раз, взяв за функцию  многочлен .

ПРИМЕР:

2. Интегралы вида , .

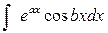Чтобы вычислить эти интегралы, надо применить метод интегрирования по частям дважды, взяв каждый раз за функцию  либо показательную функцию, либо тригонометрическую функцию.

 ПРИМЕР:

Приравняем начало и конец данной записи и из получившегося равенства выразим данный интеграл:

3. Интегралы вида , , , , , 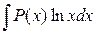где b ≠0 – действительное число.

Чтобы вычислить эти интегралы, надо применить метод

интегрирования по частям, взяв за функцию

 функцию , , , ,

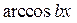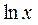
ПРИМЕР: