Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Повторение по теме «Формулы сокращенного умножения»

7 класс. Алгебра. 26.05.2021

Тема: Повторение. Формулы сокращенного умножения.

Цель: повторить применение формул сокращенного умножения.

1. Повторение по теме «Формулы сокращенного умножения»

«Тысячи неразгаданных тайн таит в себе наука, и без вас, без вашей молодости, смелости, энтузиазма, они не будут разгаданы. Наука ждёт вас, друзья».

А. С. Несмеянов

Сегодня на уроке мы повторим формулы сокращённого умножения.

Формулы сокращённого умножения:

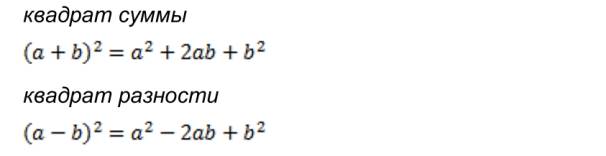
разность квадратов

.

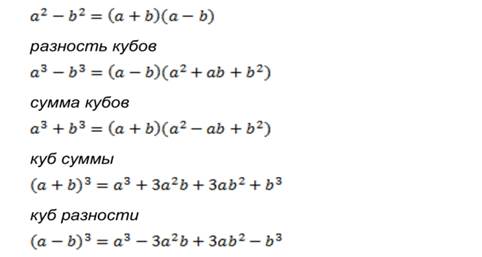
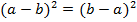
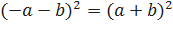2 .Решение упражнений с прямым применением формул( разбирайтесь с решением, записывайте в тетрадь).

№1. Представить в виде многочлена (формула разности квадратов двух выражений может работать как слева направо, так и справа налево).

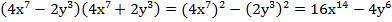
Комментарий: в данном примере произведение разности двух выражений на их сумму мы свернули в формулу разности квадратов двух выражений.

№2. Разложение на множители (нужно определить, квадратом какого выражения является первый одночлен и второй):

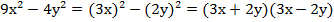
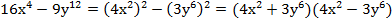
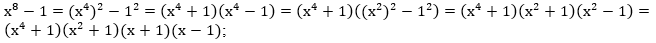
Комментарий: в последнем примере нужно несколько раз применить формулу разности квадратов.

№3.Представить в виде многочлена стандартного вида.

.

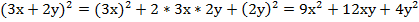Комментарий: пример решен с применением формулы квадрата суммы.

№4. Представить в виде многочлена стандартного вида.

.

№5. Представить в виде многочлена стандартного вида.

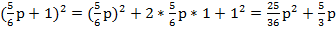+1.

№6. Представить в виде многочлена стандартного вида.

.

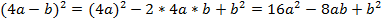№7. Представить в виде многочлена стандартного вида.

.

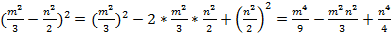№8*. Представить в виде многочлена стандартного вида.

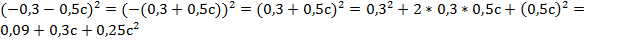
Формулы квадрата суммы и квадрата разности могут работать как слева направо, так и справа налево. Рассмотрим примеры, в которых нужно разложить заданный многочлен на множители, применяя формулы квадрата суммы и квадрата разности. Для этого нужно очень внимательно посмотреть на многочлен и определить, как именно его правильно разложить.

№9.

.

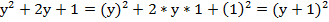Комментарий: для того, чтобы разложить многочлен на множители, нужно определить, что представлено в данном выражении. Итак, мы видим квадрат 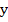и квадрат единицы. Теперь нужно найти удвоенное произведение – это 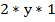. Итак, все необходимые элементы есть, нужно только определить, это квадрат суммы или разности. Перед удвоенным произведением стоит знак плюс, значит, перед нами квадрат суммы.

№10.

.

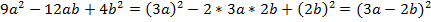№11.

.

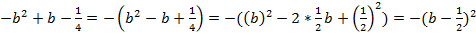Комментарий: для решения данного примера нужно вынести минус за скобки, чтобы можно было увидеть нужную нам формулу.