
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая часть.
Практическая часть.
Пример 1. Исследовать функцию и построить её график 
Решение.
1. D(y)=R.
2. Исследуем функцию на чётность и нечётность:
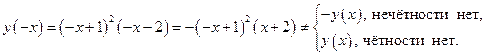
Таким образом, 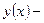 функция общего вида, симметрии у графика нет.
функция общего вида, симметрии у графика нет.
3. Точки пересечения с осями координат:
а) с осью ОХ: 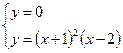 б) с осью ОУ:
б) с осью ОУ: 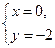 , т.е. С(0;-2).
, т.е. С(0;-2).
 , т.е. А(-1;0), В(2;0)
, т.е. А(-1;0), В(2;0)
4. Асимптоты.
а) вертикальных асимптот нет, т.к. нет точек разрыва
б) наклонные асимптоты: 
 наклонных асимптот нет.
наклонных асимптот нет.
5. Периода нет, т.к. 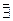 Т:
Т: 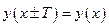 .
.
6. Промежутки монотонности.
Найдём 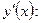
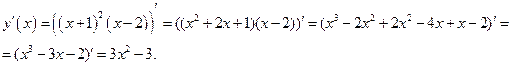
Найдём критические точки, т.е. точки, в которых 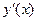 =0 или
=0 или 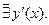
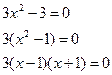
 критические точки I рода.
критические точки I рода.
Составим и заполним таблицу:
| х | 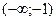
| -1 | 
| 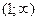
| |
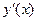
| + | - | + | ||
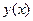
| 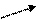
| 
| -4 | 
|
max min
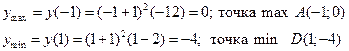
7. Промежутки выпуклости и вогнутости графика функций.
Найдём 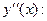
 .
.
Найдём критические точки, т.е. точки, в которых 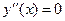 или
или 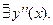
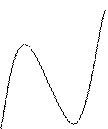
 6х=0 у
6х=0 у
|






 Составим и заполним таблицу:
Составим и заполним таблицу:
| х | 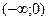
| 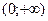
| |

| - | + | |
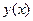
| 
| -2 | 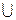
|

 | |||
 | |||



|

перегиб
у(0)=(0+1)2(0-2)=-2; точка перегиба С(0;-2)
8. Построим график функции, вычислив значение в дополнительной точке х=-2:
| х | -2 |
| у | -4 |
Пример 2. Исследовать дробно-рациональную функцию и построить её график 
Решение:
1. 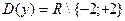
2. Исследуем функцию на четность и нечетность:
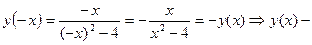 функция нечётная, и следовательно, график функции симметричен относительно точки О (0;0).
функция нечётная, и следовательно, график функции симметричен относительно точки О (0;0).
3. Точки пересечения с осями координат.
а) с осью ОХ: 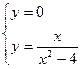
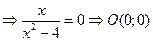
б) с осью ОУ: 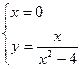

4. Асимптоты
а) вертикальные асимптоты:
х=2 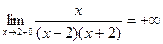 ;
; 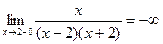
 вертикальная асимптота
вертикальная асимптота
х=-2 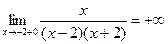 ;
; 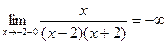
б) наклонные асимптоты: 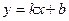
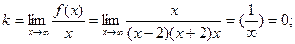
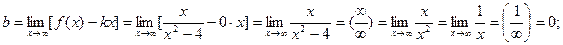
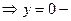 горизонтальная асимптота.
горизонтальная асимптота.
5. Периода у функции нет, т.к. 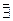 Т:
Т: 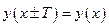 .
.
6. Промежутки монотонности.
Найдём 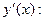

Т.к. 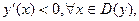 то функция убывает всюду в области определения.Точек экстремума у функции нет.
то функция убывает всюду в области определения.Точек экстремума у функции нет.
7. Промежутки выпуклости и вогнутости графика функции
Найдём 
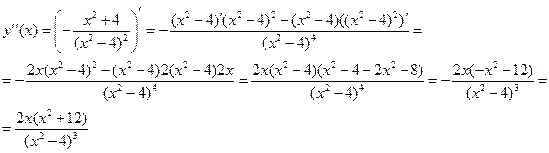
Найдём критические точки, т.е. точки, в которых 
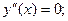
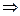
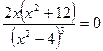 ;
; 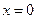
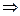
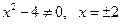
Итак, критические точки:
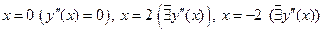 .
.
Составим и заполним таблицу, учитывая симметрию графика функции:
| х | 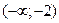
| -2 | 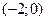
| (0;2) | (2;+ 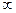 ) )
| ||

| - | 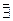
| + | - | 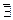
| + | |
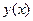
| 
| 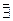
| 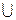
| 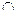
| 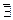
| 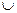
|
8. Построим график функции, вычислив значения в дополнительных точках:
| х | -3 | -1 | ||
| у | 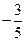
| 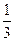
| – 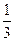
| 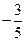
|


 у
у

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|