СВОЙСТВА ПЛАНА СКОРОСТЕЙ

§ 5. СВОЙСТВА ПЛАНА СКОРОСТЕЙ

Рассматривая схему механизма (рис. 2) и план скоростей (рис. 3), можно выявить интересные свойства плана скоростей, имеющие практическое приложение.

1. Каждое подвижное звено механизма изображается на плане скоростей одноименным подобным контуром, повернутым относительно звена на 90°, а все неподвижные шарниры механизма — его полюсом.

Рис.4. Изображающие свойства плана скоростей.

Действительно, шатун 2, взятый в виде жесткого треугольника ABD, изображается на плане скоростей одноименным заштрихованным треугольником abd, стороны которого перпендикулярны (по построению плана скоростей) соответствующим сторонам треугольника;, ABD. Шатун DE, взятый в виде прямой линии на схеме механизма,, изображается одноименным прямолинейным отрезком 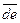, перпендикулярным звену DE.

Неподвижные шарниры механизма О₁ и О₂ изображаются на плане скоростей его полюсом, кривошип О₁А —отрезком 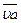^ звену О₁А, а коромысло ВО₂ — отрезком 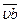, ^ звену ВО₂.

Это свойство плана скоростей, носящее название теоремы подобия, позволяет легко и просто находить скорости любых точек звеньев.

Возьмем механизм, представленный на рис. 4, а и построим для него план скоростей (рис. 4,б). Допустим, что сторона СB шатуна 2 имеет продолжение BD. Тогда для определения скорости точки D, на основании теоремы подобия, необходимо на плане скоростей продолжить отрезок 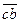за точку b и отложить на нем величину 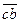, определяемую из пропорции

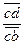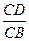
Соединив точку d с полюсомu, найдем отрезок 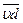, изображающий скорость V_D точки D механизма, в масштабе плана скоростей. Сравнивая треугольник аbс плана скоростей (рис. 4,б) с треугольником АВС схемы механизма (рис. 4, а), устанавливаем, что они не только подобны по перпендикулярности сторон, но и сходственно расположены. Сходственным называется такое расположение подобных фигур, когда обвод контуров этих фигур в определенном направлении, например, в направлении часовой стрелки, дает на обеих фигурах одинаковую последовательность букв, расставленных в вершинах их равных углов и служащих для обозначения этих контуров. Например, обвод контура треугольника АВС на схеме механизма в направлении часовой стрелки дает последовательность букв АСВА; ту же последовательность букв дает обвод треугольника abc по часовой стрелке на плане скоростей, а именно асbа.

На рис. 4, б пунктиром изображен треугольник ac'b, тоже подобный треугольнику АСВ на рис. 4, а, так как три стороны ê ac'b перпендикулярны трем сторонам ê ACB, но в данном случае ê ac'b не является сходственно расположенным по отношению к ê ACB. Обвод контура треугольника ac'b по часовой стрелке дает последовательность букв abc'а, т. е. не совпадает с последовательностью букв ê АСВ при обводе также по часовой стрелке.

На основании рассмотренного примера можно сделать очень важный вывод, облегчающий нахождение скоростей точек механизма. Если с помощью плана скоростей найдены скорости двух точек звена, то скорость любой другой точки этого звена может быть найдена без составления уравнений скоростей на основании теоремы подобия. Для этого необходимо на изображающем отрезке или контуре взять соответственно расположенную точку и соединить ее с полюсом плана скоростей. Найденный отрезок будет представлять абсолютную скорость данной точки в масштабе к_u плана скоростей. Очевидно, не требуется составлять уравнения скоростей и для точки С звена АСВ, если известны скорости точек А и В. Достаточно на отрезке 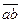плана скоростей построить подобный и сходственно расположенный треугольник abc.

2. Отрезки плана скоростей, проходящие через полюс u, изображают абсолютные скорости точек механизма. Абсолютные скорости всегда направлены от полюса. Отрезки плана скоростей, не проходящие через полюс, изображают относительные скорости (в данном случае вращательные), направленные всегда к той букве плана скоростей, которая стоит первой в обозначении скорости. Например, скорость V_BA направлена от точки а к точке b (рис. 4,6); скорости V_CA и V_CB направлены от точек а и b к точке с.

3. Как уже отмечалось, неподвижные точки механизма, скорости которых равны нулю, изображаются на плане скоростей полюсом u. Звено, совершающее сложное плоское движение, например звено АСВ (рис. 4, а), будет иметь абсолютный мгновенный центр вращения P₂₄, скорость которого равна нулю. На плане скоростей этот мгновенный центр также изображается полюсом. Если на стороне AB треугольника АСB (рис. 4, а) построить êABu₀, подобный êabu плана скоростей и сходственно с ним расположенный, то вершина u₀ треугольника будет определять мгновенный центр вращения.

Подвижные шарнирные точки механизма А, В, С, D изображаются на плане скоростей концами векторов абсолютных скоростей, т. е. точками а, b, с и d.

4. План скоростей дает возможность находить касательные и нормали к траекториям точек механизмов. Так, например, скорость 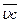точки С показывает направление касательной t—t (рис. 4, а) к траектории этой точки, а перпендикуляр к скорости 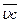определяет направление нормали п—п. Точно так же могут быть определены касательная и нормаль к траектории движения точки D.

12 Следующая ⇒