Площадь криволинейной трапеции выражается интегральной суммой или числом, которое называется определенным интегралом.

Тема урока: Виды криволинейных трапеций. Вычисление площадей криволинейных трапеций с помощью определенного интеграла. Свойства определенного интеграла.

«Благодаря этому исчислению всё предстаёт перед очами и в уме с восхитительной краткостью и ясностью», Г. Ф. Лейбниц

Цель урока : - повторить теоретический материал;

-обобщить и систематизировать знания для нахождения первообразных;

-отработать навыки вычисления интегралов, площадей криволинейных трапеций.

Понятие определенного интеграла выводится через криволинейную трапецию.

Фигура, ограниченная отрезком оси абсцисс (у=0) , отрезками вертикальных прямых x=a , x=b и графиком непрерывной неотрицательной на отрезке функции f(х), называется криволинейной трапецией.

Площадь криволинейной трапеции выражается интегральной суммой или числом, которое называется определенным интегралом.

Определенный интеграл вычисляется по формуле Ньютона – Лейбница:

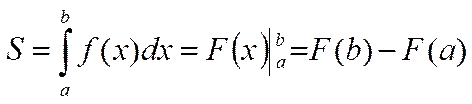Виды криволинейных трапеций и формулы для нахождения их площадей.

1. (1)

2. (2)

3. (3)

Задание №1

Вычислите площадь криволинейной трапеции, ограниченной линиями:

у = х + 3, у = 0, х = 1 и х = 3.

Решение: Нарисуем линии, заданные уравнениями, и заштрихуем криволинейную трапецию, площадь которой будем находить. Так как функция у = х + 3 на заданном интервале от 1 до 3 положительна, то площадь криволинейной трапеции будем находить по формуле (1).

Площадь измеряетсявквадратных единицах,поэтому в ответе пишем: кв.ед.

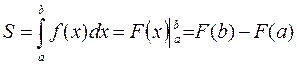Определенный интеграл вычисляется по формуле Ньютона – Лейбница:

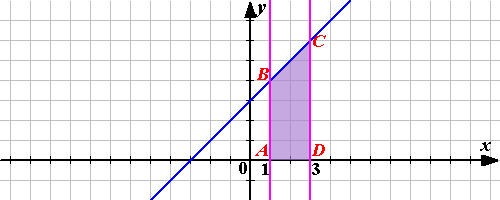
S_АВСД= 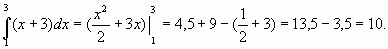(кВ.ед)

Ответ: 10 кв.ед.

Кроме умения вычислять определенный интеграл, нам нужно вспомнить свойства площадей. В чем они заключаются?

Равные фигуры имеют равные площади.
Если фигура разбита на две части, то её площадь находится как сумма площадей отдельных частей.

12 3 Следующая ⇒