Теорема 7. Если одна из двух параллельных прямыхa∥bпараллельна данной плоскостиα, то другая прямая либо параллельна этой плоскости, либо лежит в этой плоскости.

Практическая работа №43

Задание1.

Начало формы

Определи взаимное расположение данной прямой и плоскости.

1. Прямая AA1 и плоскость (CBB1): прямая параллельна плоскости прямая пересекает плоскость прямая находится в плоскости .

2. Прямая BC и плоскость (ABC): прямая пересекает плоскость прямая параллельна плоскости прямая находится в плоскости .

3. Прямая CC1 и плоскость (ABD): прямая пересекает плоскость прямая параллельна плоскости прямая находится в плоскости .

4. Прямая CB1 и плоскость (DD1C): прямая параллельна плоскости прямая находится в плоскости прямая пересекает плоскость .

5. Прямая AB1 и плоскость (BCD): прямая параллельна плоскости прямая пересекает плоскость прямая находится в плоскости .

Задание 2.

Конец формы

Начало формы

Основание AB трапеции ABCD лежит в плоскости α. Основание CD не лежит в этой плоскости.

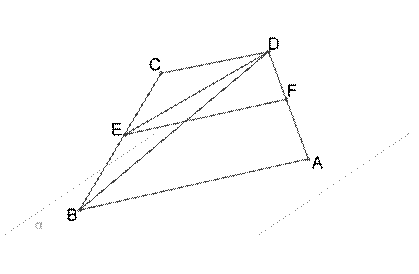
Дополни данные предложения, которые характеризуют взаимное расположение данных прямых и плоскости α.

1.Tак как прямая DB имеет общую точку с данной плоскостью, то эта прямая пересекается с плоскостью находится в плоскости параллельна плоскости α.

2.Прямая CD параллельна прямой AB в данной плоскости, значит, она пересекается с плоскостью параллельна плоскости находится в плоскости α.

Задание 3.

Дан треугольник ABC. На сторонах AB и AC соответственно отложены точки D и E так, что DE= 3 см и 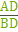= . Через точки B и C проведена плоскость α, которая параллельна отрезку DE.

Сторона BC равна см.

Конец формы

⇐ Предыдущая 12