Опр-е. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Внимание!

Теорию записать с чертежами, задания выполнить.

Тема. Параллельность прямой и плоскости

Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:

1) прямая лежит (находится) в плоскости;

2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются);

3) прямая и плоскость не имеют общих точек.

Опр-е. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема 5 «Признак параллельности прямой и плоскости». Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

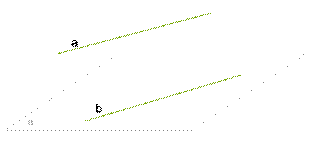
Доказательство:
доказательство проведём от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причём A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b — скрещивающиеся.

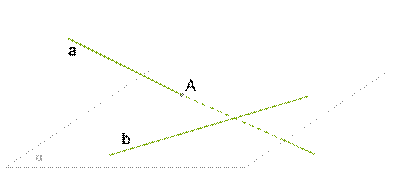
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Обрати внимание!

Следующие две теоремы очень часто используются при решении задач.

Теорема 6. Если плоскостьβпроходит через данную прямуюa, параллельную плоскостиα, и пересекает эту плоскость по прямойb, тоb∥a.

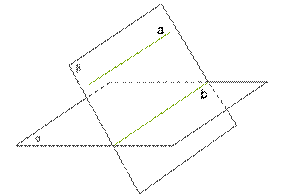
Обрати внимание!

Прямую b иногда называют следом плоскости β на плоскости α.

12 Следующая ⇒