Тема 8. Метод наименьших квадратов и его использование для расчета параметров уравнений тренда и регрессии

Тема 8. Метод наименьших квадратов и его использование для расчета параметров уравнений тренда и регрессии

8.1. Сущность метода наименьших квадратов

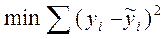Метод наименьших квадратов подробно изучается в математической статистике. Его сущность заключается в том, что параметры аналитической функции, используемой для сглаживания ряда, подбираются таким образом, чтобы минимизировать сумму квадратов отклонений расчетных (теоретических) значений динамического ряда от фактических (исходных) значений. То есть находится:

Такая сумма квадратов может быть представлена как функция многих переменных, в качестве которых выступают параметры уравнений тренда (или регрессии). То есть задача поиска параметров функций, сглаживающих исходный ряд, преобразуется в задачу поиска min Q (a₁, a₂, a₃,…a_n)

Как известно из высшей математики, задача поиска экстремума (минимума или максимума) некоторой функции обычно решается путем ее дифференцирования и приравнивания производных к нулю. Точно так же данная задача решается и в этом случае. Находятся частные производные функции Q (a₁, a₂, a₃,…a_n) по каждому из параметров и приравниваются к нулю. Получается система уравнений, в которой число неизвестных и параметров совпадает с числом параметров, которые необходимо найти. Эта система в статистике называется системой «нормальных уравнений».

8.2. Расчет параметров уравнений тренда

Расчет параметров уравнения тренда осуществляется с помощью известного метода наименьших квадратов, суть которого изложена в 8.1. Для расчета строится вспомогательная таблица, в которой вводится так называемое условное обозначение времени. Его вводят таким образом, чтобы Σt = 0. Если число реальных периодов (моментов) времени нечетное, в середине ставится 0, а затем отсчет ведется вправо и влево от нуля (как считают в истории «годы до нашей эры»). Если число периодов четное, то 0 пропускается; при этом отсчет вправо ведется от 1, отсчет влево – от –1. Пример условного обозначения показан времени в таблице 8.2.1, приведенной ниже.

12 Следующая ⇒