Свойства функции F(x). Следствие 2

Свойства функции F(x)

1. Значения интегральной функции принадлежат отрезку [0;1], т.е.

0£F(x) £1 (4)

Доказательство:

Так как по определению F(x) - это вероятность Р(Х<х), а вероятность всегда есть число неотрицательное, не превышающее 1.

2. F(x)- функция неубывающая, т.е.

F(x₂) ³ F(x₁), если x₂ > x₁

Доказательство:

Рассмотрим событие Х<х₂. Оно может быть представлено в виде суммы двух несовместных событий, т.е. (или Х<х₁, или х₁£Х<х₂ ).

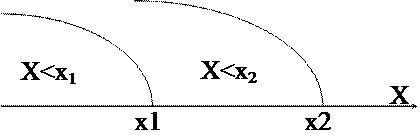х₁£Х<х₂

Применим теорему сложения вероятностей для несовместных событий.

Р (Х<х₂ )= Р (Х<х₁)+ Р (х₁£Х<х₂)

отсюда

Р (Х<х₂ )-Р (Х<х₁)=Р (х₁£Х<х₂) или

F(x₂) -F(x₁) = Р (х₁£Х<х₂) (*)

Так как любая вероятность есть число неотрицательное, то:

F(x₂) -F(x₁)³ 0 или F(x₂) ³ F(x₁).

Следствие 1. Вероятность попадания СВ Х в заданный интервал.

Вероятность того, что СВ Х примет значение, заключенное в интервале ] a;b [ равна приращению интегральной функции на этом интервале, т.е.

P(α£X<b)=F(α)-F(b) (5)

Это следует из равенства (*) при Х1 = a Х2= b.

Следствие 2

Вероятность того, что непрерывная СВ примет одно определенное значение, равна нулю, т.е.

P(X=x_i)=0 (6)

Доказательство:

Пусть Х- непрерывная СВ. Рассмотрим формулу 1 следствия:

Р(a £ Х<b) = F(b)- F(a).

Пусть a=Х1, а b= х₁+ Dх. Тогда

Р(х₁£ х < х₁+ Dх)= F(x₁+ Dх) -F(x₁) .

Пусть Dх®0. Так как Х- непрерывная СВ, то функция F(x) - непрерывная. В силу непрерывности F(x) в точке х₁разность F(x₁+ Dх) -F(x₁) будет ®0 и, следовательно, [F(x₁+ Dх) -F(x₁)]=0;

а Р(х₁£ х < х₁+ Dх)=Р (х=х₁).

Итак, Р (х=х₁)=0.

Используя это положение, можно доказать справедливость равенства.

Р(a £ Х<b)= Р(a < Х<b) = Р(a<Х£ b)=

= Р(a £ Х£ b) (7)

При определении вероятности того, что непрерывная и т.д. СВ попадет в интервал, можно не делать различия между случаями, когда концы интервала принадлежат или не принадлежат интервалу .

3. Если возможные значения СВ принадлежат отрезку [a;b], то:

1) F(x) =0 при х £ a

2) F(x) =1 при х> b .

Следствие: Если возможные значения непрерывной СВ расположены на всей оси ОХ, то справедливы следующие предельные соотношения:

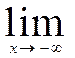F(x) =0;

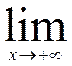F(x) =1

или

F(-¥)= 0, (8’)

так как событие (Х<-¥) = Æ и

F(+¥)=1, (8”)

так как событие (Х<+¥)=W.

4. Вероятность того, что СВ Х примет значение, большее или равное х, равна разности между единицей и функцией распределения при этом значении х. т.е. Р (Х³х)=1 - F(x) (9)

Доказательство:

События (Х³х) и (Х<х) - противоположные, поэтому

Р (Х³х)+ Р(Х<х)=1

Р (Х³х) =1- Р(Х<х),

т.е. Р (Х³х) =1- F(x)

⇐ Предыдущая 12