Формула прямоугольников

У-17

Тема: «Приближенное вычисление по формулам прямоугольников, трапеций и формуле Симпсона»

Цель занятия:рассмотреть правила вычисления интегралов по формулам Симпсона, трапеции, прямоугольников.

Пусть требуется найти определенный интеграл 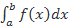, причем функция y=f(x) считается непрерывной на отрезке [a;b]. Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:

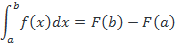
Но не в каждом случае отыскание первообразной для подынтегральной функции является достаточно простым, а также не для всякой непрерывной функции существует первообразная, выражающаяся через элементарные функции. В подобных случаях применяют приближенные формулы, которые позволяют вычислить определенный интеграл с любой степенью точности.

Наиболее часто используются три формулы приближенного вычисления определенного интеграла –

· формула прямоугольников,

· формула трапеций и

· формулу парабол или формула Симпсона,

основанные на геометрическом смысле определенного интеграла: если функция непрерывна и положительна на отрезке, то определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями и (рис. 1).

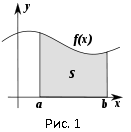
1. Формула прямоугольников

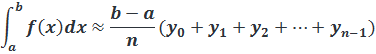
Или

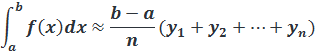
2. Формула трапеций:

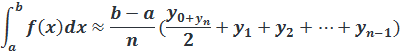
3. Формула Симпсона

))

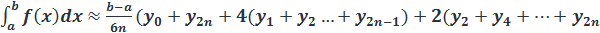ПРИМЕР: Вычислить методом трапеции , разделив отрезок [0;2] на 20 равных частей

12 Следующая ⇒