Задачи для решения

Задачи для решения

Задача 1.Прямая РQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках Р₁ и Q₁. Докажите, что PQ = P₁Q₁.

Задача 2. Прямая ОА перпендикулярна к плоскости ОВС, и точка О является серединой отрезка АD. Докажите, что АВ=DB.

Задача 3. Через точку О пересечения диагоналей квадрата, сторона которого равна 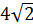дм, проведена прямая ОК, перпендикулярная к плоскости квадрата. Найдите расстояние от точки К до вершин квадрата, если ОК= 3 дм.

Задача со звёздочкой (необязательная к решению). В треугольнике АВС дано: ∠С=90⁰, АС=6 см,ВС=8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК=12 см. Найдите КМ.

⇐ Предыдущая 12