Тема: Правильная пирамида.. Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава III, § 2, п. 32), законспектировать решённые задачи, решить задачи самостоятельной работы и ответ
Тема: Правильная пирамида.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава III, § 2, п. 32), законспектировать решённые задачи, решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
- Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий центр основания с вершиной пирамиды является её высотой.
Все боковые рёбра правильной пирамиды равны между собой.
Боковые грани правильной пирамиды – равнобедренные треугольники.
Высота боковой грани правильной пирамиды называется апофемой.
Апофемы правильной пирамиды равны между собой.
Построение правильной пирамиды
1. Начнём с правильной треугольной пирамиды.
При изображении величины углов, их равенство не сохраняется, поэтому правильный (равносторонний) треугольник изображаем произвольным треугольником ABC.
Центр правильного треугольника – в точке пересечения его медиан. Медиана делит сторону пополам, а отношение отрезков на одной прямой сохраняется, поэтому медианы не искажаются. Проведём две медианы в треугольнике ABC: AK и C, обозначим центр треугольника – О. Через точку О проведём вертикальный отрезок, изображающий высоту пирамиды, и соединим верхний конец отрезка – точку D с вершинами треугольника ABC. ABCD – изображение правильной треугольной пирамиды.
2. Аналогично, строим правильную четырёхугольную пирамиду.
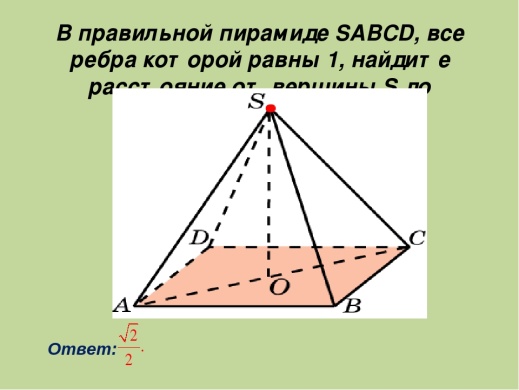 В снованииправильной четырёхугольной пирамиды – квадрат, который изображаем, по правилам параллельного проектирования, параллелограммом. Через центр основания ABCD – точку O проводим вертикально высоту пирамиды SO и соединяем вершину пирамиды S с вершинами основания ABCD.
|
