Хелпикс

Главная

Контакты

Случайная статья



Практическая работа. Составление различных типов уравнения прямой.. Решение аналитических задач на плоскости. Краткая теория

Стр 1 из 2Следующая ⇒


Практическая работа

Составление различных типов уравнения прямой.

Решение аналитических задач на плоскости

Цель: научиться составлять уравнения прямых, заданных разными способами, и уравнения плоскостей.

Краткая теория

Уравнение плоскости, проходящей через точку (x0;y0;z0),перпендикулярно вектору имеет вид .

Раскрыв скобки в данном уравнении получим:

.

    Обозначив через D, получим уравнение

,   (1).

    Данное уравнение называют общим уравнением плоскости.

Особые случаи уравнения (1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Способы задания уравнения прямой в пространстве:

1)векторное уравнение прямой имеет вид , где  - координаты вектора , перпендикулярного данной прямой,  - координаты точки М, принадлежащей данной прямой;

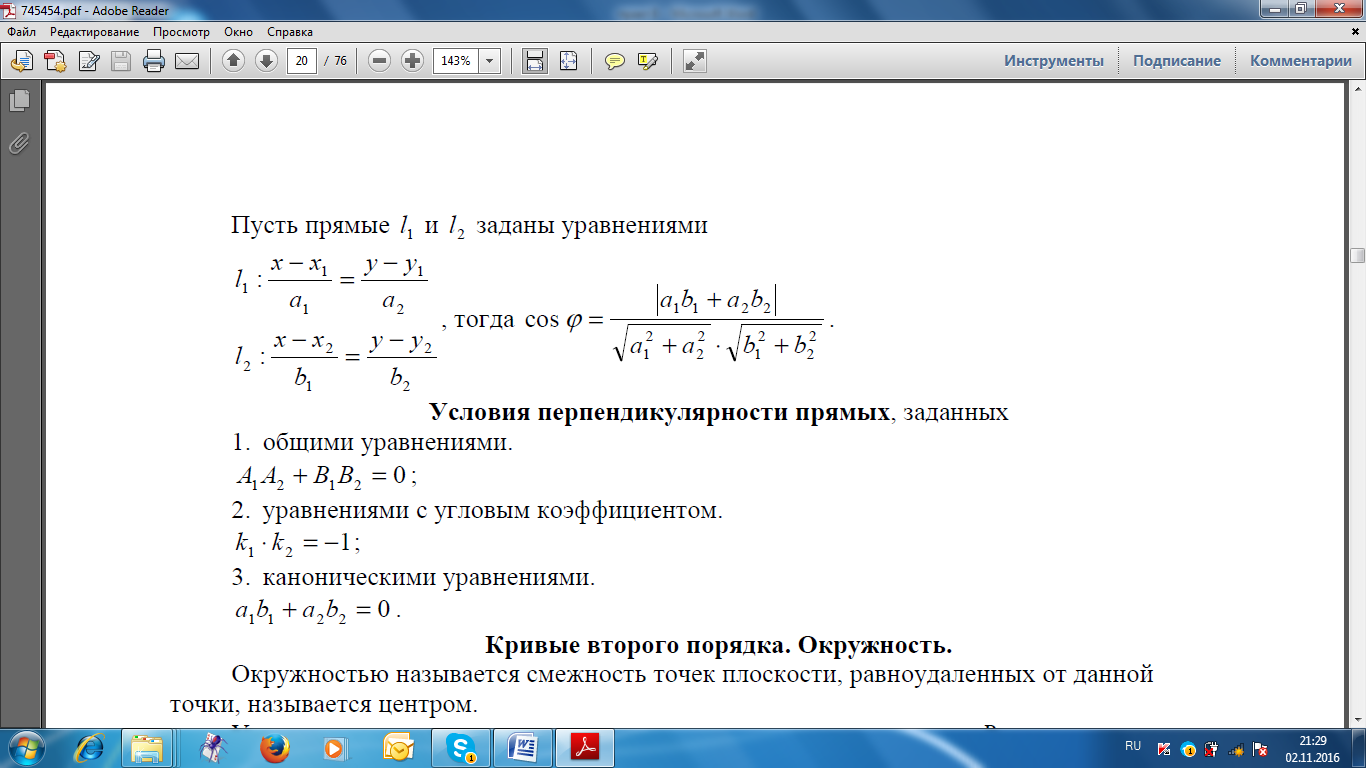
2)каноническое уравнение прямой - ,

3)параметрическое уравнение прямой -  где  - координаты точки М, принадлежащей данной прямой,  - координаты вектора, параллельного прямой;

4)уравнение прямой, проходящей через две данные точки А(х1;y1;z1) и В(х2;y2;z2):

;

    5) как пересечение двух плоскостей, т.е. система уравнений:

A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0.

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.