
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
если a= , уравнение примет вид 0х= , нет решений;
(2a-3)(2a+3)=0
a=  или a=
или a= 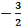
если a= , уравнение примет вид 0х= , нет решений;
если a= , уравнение примет вид 0х= , нет решений.
2) 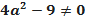 , тогда
, тогда 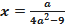
Ответ: если a=  , a=
, a= 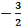 нет решений,
нет решений,
если a 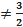 , a
, a 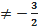 ,
, 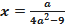
22. Решить уравнение относительно переменной х
Решение: преобразуем данное уравнение 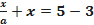
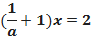
1) если a=0 , нет решений;
2)если , то есть a=-1, тогда уравнение примет вид 0x=2. Это уравнение решений не имеет.
3)если 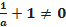 , то есть a
, то есть a 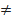 -1 и a
-1 и a 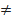 0,
0, 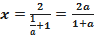
ответ: если а=0, а=-1, уравнение не имеет решений,
a 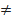 -1 и a
-1 и a 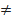 0,то
0,то 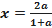
23. Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.
Решение:
Раскроем скобки: aх – а + 2х – 2 = 0
Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое число.
Ответ: при а ≠ -2 х = 1;
при а = -2 х- любое число.
24. Решить уравнение 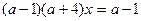
Решение:
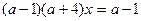
1) Если 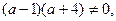
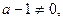
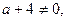
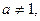
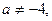 то уравнение имеет единственное решение
то уравнение имеет единственное решение 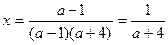
2) Если 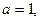 то уравнение принимает вид:
то уравнение принимает вид: 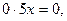
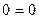 (верно)
(верно)
Значит наше уравнение имеет бесконечное множество решений.
3) Если 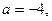 то уравнение принимает вид:
то уравнение принимает вид: 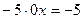 ,
, 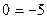 (не верно)
(не верно)
Значит первоначальное уравнение не имеет корней.
Ответ: при 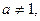
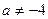 одно решение
одно решение 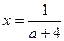
при 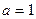 нет решений
нет решений
при 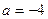 х-любое число.
х-любое число.
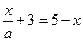 |
25. 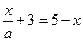 Решите уравнение .
Решите уравнение .
Решение.
Данное уравнение заменим равносильным ему:
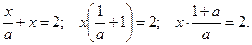 |
При а = 0 уравнение не имеет смысла.
При а 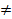 0 и а + 1 = 0 (а = – 1) уравнение примет
0 и а + 1 = 0 (а = – 1) уравнение примет 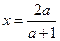 вид 0·х = 2, т. е. не имеет решений.
вид 0·х = 2, т. е. не имеет решений.
При а 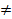 0, а
0, а 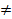 1 уравнение имеет единственный корень .
1 уравнение имеет единственный корень .
Ответ: если а = 0, то уравнение не имеет смысла;
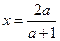 если а
если а 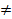 0 и а
0 и а 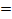 – 1, то корней нет;
– 1, то корней нет;
если а 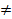 0, а
0, а 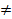 1, то
1, то
.
26. При каком значении параметра a, х=2,5 является корнем уравнения х+2= a+7?
Так как х=2,5 корень уравнения х+2= a+7, то при подстановке х=2,5 в уравнение получим верное равенство 2,5 +2= a+7, откуда находим a= -2,5.
Ответ: при a=-2,5.
27. При каком значении параметра а корнем уравнения ax−100x=a−100 является любое число?
Решение
Преобразуем данное уравнение к виду (a−100)x=a−100, используя распределительное свойство умножения
Определим контрольное значение параметра: a−100=0, a=100При a=100 уравнение имеет вид 0·x=0, решением которого является любое действительное число.
Ответ: при a=100 x-любое число.
28. При каком значении параметра s уравнение (3−2s)x=0 имеет единственное решение?
Решение
Определим контрольное значение параметра: 3−2s=0, s=1,5
При s≠1,5 уравнение имеет один корень x =0
Ответ: при s≠1,5, уравнение имеет единственное решение.
29. При каком значении параметра k, уравнение 2·x = 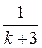 не имеет корней?
не имеет корней?
Решение.
При k=−3 знаменатель дроби уравнения обращается в нуль, поэтому уравнение не имеет смысла.
Ответ: при k=−3 уравнение теряет смысл.
30. Найдите значение а, при котором число 3 является корнем уравнения
а(1 + х) – х(1 – а) = 4.
Решение: упростим правую часть уравнение а+х-х+ах=4
Уравнение примет вид: а+ах=4
Подставим вместо х число 3, получим 4а=4. Отсюда следует, что а=1.
31. Найти все значения параметра a, при которых корни уравнения 6x−5a=15лежат на отрезке [−5;5]
Решение:
1 способ (аналитический) преобразуем уравнение 6х=15+5а, х= 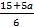 , нужно найти корни, которые лежат на отрезке [−5;5]. Для этого запишем двойное неравенство и преобразуем его (для этого потребовалось изучение материала 8 класса)
, нужно найти корни, которые лежат на отрезке [−5;5]. Для этого запишем двойное неравенство и преобразуем его (для этого потребовалось изучение материала 8 класса)
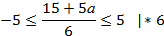
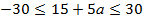
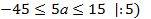
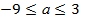
Ответ:при 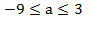 корни уравнения6x−5a=15лежат на отрезке [−5;5]
корни уравнения6x−5a=15лежат на отрезке [−5;5]
1 способ (графический). График x(a) для этого же примера на рисунке 4.
Иногда для решения удобно построить график зависимости a(x):a= 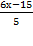 . Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что a∈[−9;3] (при x=5⇔a=3; и при x=−5⇔a=−9)
. Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что a∈[−9;3] (при x=5⇔a=3; и при x=−5⇔a=−9)

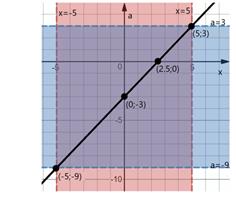
Рисунок 5. Графическая интерпретация решения уравнения
Ответ:при 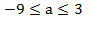 корни уравнения 6x−5a=15лежат на отрезке [−5;5]
корни уравнения 6x−5a=15лежат на отрезке [−5;5]
32. При каких значениях параметра а корни уравнения 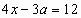 принадлежат отрезку [1; 3]”?
принадлежат отрезку [1; 3]”?
Используем графики функций 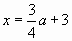 или
или 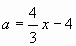 . (Рис. 3, 4).
. (Рис. 3, 4).
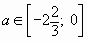 (если
(если 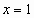 , то
, то 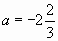 ; если
; если 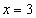 , то
, то 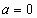 ).
).
А теперь построим семейство графиков функции 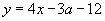 в системе координат (хОу) (они параллельны прямой
в системе координат (хОу) (они параллельны прямой 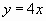 , где
, где 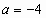 ). (Рис. 5).
). (Рис. 5).
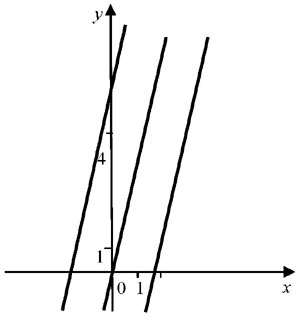
Решениями уравнения 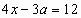 являются абсциссы точек пересечения с осью Ох графиков функции
являются абсциссы точек пересечения с осью Ох графиков функции 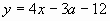 при заданных значениях параметра а. Если
при заданных значениях параметра а. Если 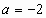 , то
, то 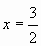 ; если
; если 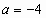 , то
, то 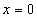 . Общее решение уравнения
. Общее решение уравнения 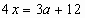 :
: 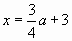 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|