Выполните задания 1 – 4 из Рабочей тетради (часть 2) (п. 25, стр. 50).

Выполните задания 1 – 4 из Рабочей тетради (часть 2) (п. 25, стр. 50).

Сложение и умножение числовых неравенств

Свойство 4.

.Т. е. любые неравенства одного знака можно складывать.

Свойство 5.

Рассмотрим перемножение неравенств.

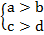
Если все числа положительные, то их можно перемножить, и получим . Если умножать на отрицательное число, то знак неравенства меняется на противоположный.

Свойство 6.

Рассмотрим возведение в степень неравенств.

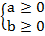и тогда .

Пример №1

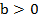Даны два положительных числа и .И 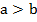. Доказать, что их обратные величины связаны противоположным неравенством: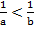

Решение. Перенесем в одну сторону и выполним необходимые действия.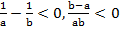

Так как даны положительные числа и 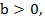то нужно убедиться, что . Чтобы дробь была отрицательным числом, надо, чтобы числитель был отрицательным числом. Умножаем 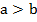на -1 и получаем .

Пример №2

Дано:

а) Оценить число

Решение: Обе части неравенства умножаем на 2. Тогда 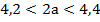. Задача решена.

б) Оценить число -3

Решение: будет меняться в пределах . Умножаем неравенство на 3. Получаем ;

в) Oценить разность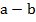

Решение: . Неравенства одного знака можно складывать. Получаем:

Ответ:

Пример №3

Дано:

Решение: Переносим все в одну сторону. . Приводим к общему знаменателю: Знаменатель по условию , значит и числитель должен быть положительным числом, т. е. . Квадрат числа всегда равен положительному числу, кроме, если а=1. Что и требовалось доказать.

⇐ Предыдущая 123 Следующая ⇒