
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Числовые неравенства. Свойство неравенств №1. Свойство неравенств №2. Свойство неравенств №3
Числовые неравенства
Данный урок посвящён теме «Свойства числовых неравенств». В ходе этого занятия вы вспомните определение неравенства. Сможете получить представление об основных свойствах числовых неравенств, которые впоследствии пригодятся для решения задач.
Что такое числовое неравенство.
Вспомним, что означают неравенства: 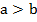 и
и 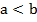 :
:
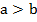 означает, что
означает, что 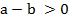 и
и 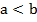 означает, что
означает, что 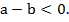
Вывод: число 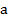 считается большим числа b, если разность
считается большим числа b, если разность 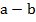 является положительным числом. Число
является положительным числом. Число 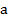 считается меньше числа b, если разность
считается меньше числа b, если разность 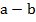 является отрицательным числом.
является отрицательным числом.
Геометрическая интерпретация.



 Если точка с координатой
Если точка с координатой 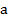 находится правее, чем точка с координатой b, значит число
находится правее, чем точка с координатой b, значит число 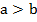 . И наоборот. Не всегда очевидна алгебраическая запись, поэтому геометрическая интерпретация часто помогает. С положительными числами это очевидно, а с отрицательными лучше пользоваться расположением этих чисел на числовой оси.
. И наоборот. Не всегда очевидна алгебраическая запись, поэтому геометрическая интерпретация часто помогает. С положительными числами это очевидно, а с отрицательными лучше пользоваться расположением этих чисел на числовой оси.
Свойства числовых неравенств.
Свойство неравенств №1
Если 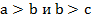 , то
, то 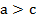
Свойство неравенств №2
Если 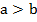 и с – любое число, то
и с – любое число, то 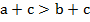 .
.
Свойство неравенств №3
Если 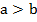 и c – положительное число, то
и c – положительное число, то 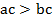 . И если
. И если 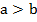 и c – отрицательное число, то
и c – отрицательное число, то 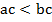 .
.
Пример: 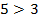 , умножим обе части неравенства на 2 и получим
, умножим обе части неравенства на 2 и получим 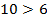 , но если обе части неравенства умножить на -2, то знак неравенства поменяется на противоположный:
, но если обе части неравенства умножить на -2, то знак неравенства поменяется на противоположный: 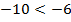 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|