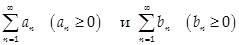- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Числовые ряды. Лекция 1. Необходимое условие сходимости ряда. Если , то (при любых ). Если сгруппировать слагаемые в сходящемся ряде, то полученный ряд тоже будет сходится. В общем случае от перестановки слагаемых сумма ряда может измениться. Ряды с неотр
Числовые ряды. Лекция 1
| I. Наводящие рассуждения |
1) Площадь квадрата.Рассмотрим квадрат со стороной 1 и будем разбивать его на части.При этом:
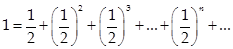
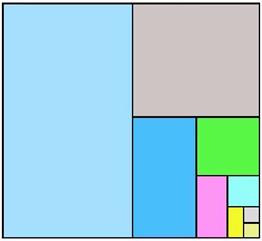
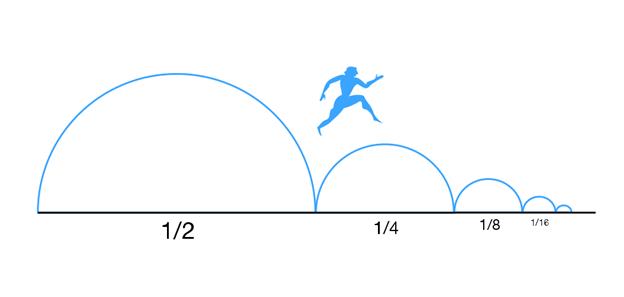
2) 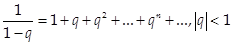
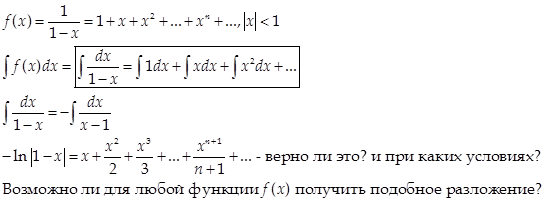
3)
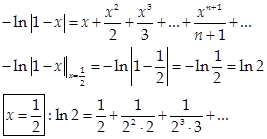
| II. Основные определения |
Определение Числовым рядом (рядом)называется выражение вида
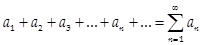 ,
,
при этом: 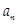 – общий член ряда;
– общий член ряда; 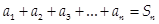 – частичная сумма ряда.
– частичная сумма ряда.
Если существует и конечен 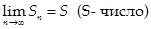 , то говорят, что ряд сходится и его сумма равна S, иначе – ряд расходится.
, то говорят, что ряд сходится и его сумма равна S, иначе – ряд расходится.
Таким образом, для того, чтобы выяснить, сходится ряд или расходится, нужно:
1) «Оборвать» его на n-ом слагаемом (т.е. получить частичную сумму Sn)
2) Вычислить предел 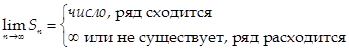
Примеры:
1)
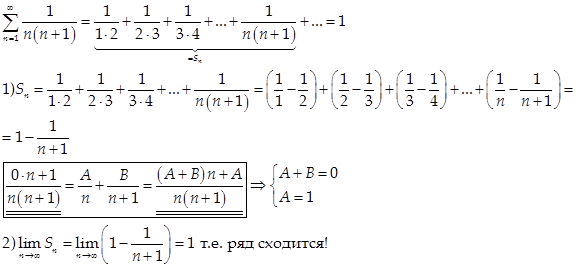
2)
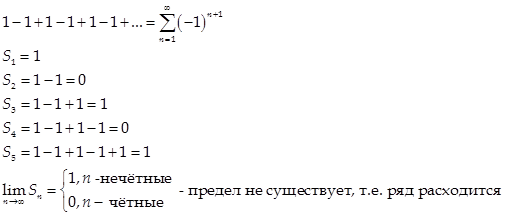
3)
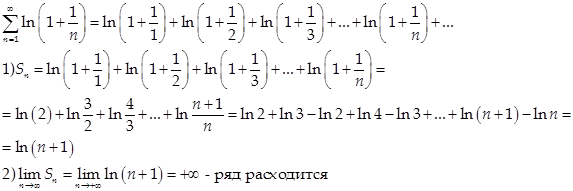
4) 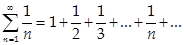
Необходимое условие сходимости ряда
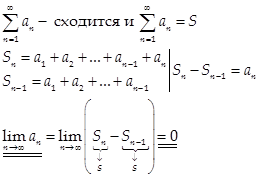
Если 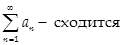 , то
, то 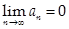
Если 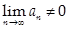 , то
, то 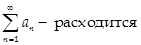
Примеры:
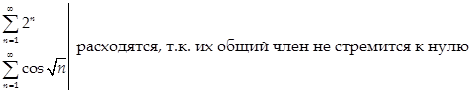
Обратное утверждение неверно! Т.е. существуют расходящиеся ряды, у которых 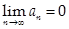 .
.
Пример: 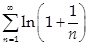 - расходится и при этом
- расходится и при этом 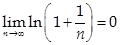
Свойства сходящихся рядов
1) Если , то (при любых )
2) Если сгруппировать слагаемые в сходящемся ряде, то полученный ряд тоже будет сходится
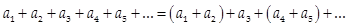
3) В общем случае от перестановки слагаемых сумма ряда может измениться
Пример:
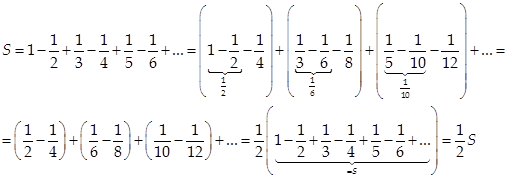
| III. Признаки сходимости рядов |
Ряды с неотрицательными членами
(1) Критерий сходимости ряда с неотрицательными членами:
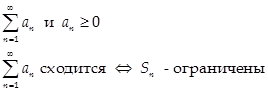
Доказательство:
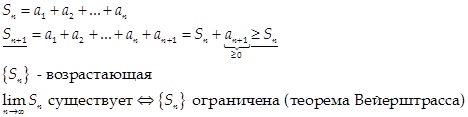
(2) Признаки сравнения
|
| |
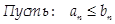 . Тогда:
(1) Если . Тогда:
(1) Если 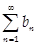 - сходится, то - сходится, то 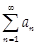 сходится;
(2) Если сходится;
(2) Если 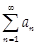 - расходится, то - расходится, то 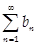 расходится расходится
| 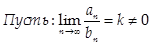 .
В этом случае ряды ведут себя одинаково (сходятся или расходятся одновременно) .
В этом случае ряды ведут себя одинаково (сходятся или расходятся одновременно)
|
Пример: 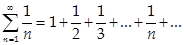 - расходится по признаку сравнения
- расходится по признаку сравнения
Пусть: 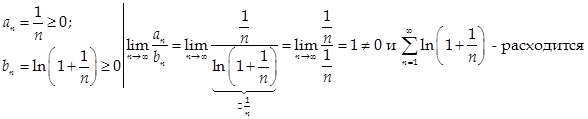
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|