Семинар 4. Магнитные свойства атомов

Семинар 4. Магнитные свойства атомов

План занятия

1. Краткое теоретическое введение

2. Разбор типовых задач (Л-3: 5.206, 5.210, 5.215)

3. Самостоятельное решение задач (5.205, 5.211, 5.220)

Теоретическая часть

Для состояний, принадлежащих данному L, S, J-мультиплету ( 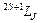), оператор магнитного момента атома можно представить в виде

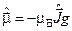, (1)

где

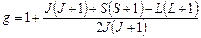(2)

называют g–фактором или фактором (множителем) Ланде, L, S, J – квантовые числа, определяющие мультиплет 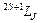, 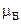‑ магнетон Бора.

Минимальное значение фактора Ланде (2) равно нулю. В этом случае магнитный момент атома тоже равен нулю, хотя его момент импульса может быть отличен от нуля. Если орбитальный момент импульса атома равен нулю (L = 0), полный момент импульса атома совпадает со спиновым моментом (J = S). Подстановка в (11) L = 0 и J = S дает g = 2 (это является результатом того, что для спина коэффициент пропорциональности между магнитным моментом и моментами импульса равен 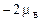). Для атомов, у которых спиновый момент импульса равен нулю (S = 0) полный момент импульса совпадает с орбитальным J = L, что с очевидностью приводит к g = 1.

Таким образом, магнитный момент многоэлектронного атома равен:

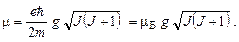
Атом в магнитном поле. Эффект Зеемана

Взаимодействие магнитного момента атома с магнитным полем приводит к приобретению атомом дополнительной энергии, оператор которой имеет вид

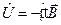, (3)

где 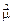- оператор магнитного момента атома (1).

Направим ось 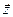вдоль вектора 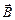при этом (3) примет вид

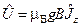. (4)

Собственными значениями оператора 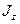являются магнитные квантовые числа ( ).

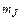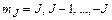Поэтому уровни энергии атома в магнитном поле:

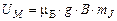(5)

Выражение (5) говорит о том, что при наложении магнитного поля состояние атома с полным моментом импульса, определяемым квантовым числом J, расщепляется на 2J+1 - состояния - происходит снятие выражения уровней мультиплета по магнитному квантовому числу.

12 Следующая ⇒