Тема: Уравнение сферы. План урока.. Ход урока. Организационный момент. Проверка домашнего задания.

Тема: Уравнение сферы

Цель: Определение шара и сферы (шаровой поверхности) и связанных с ним понятий (центр, радиусы, диаметры, диаметрально противоположные точки). Рассмотреть уравнение сферы.

Оборудование: плакаты, модели шара, сферы.

План урока.

1) Организационный момент.

2) Проверка домашнего задания.

3) Повторить определение окружности, уравнение окружности. Решить устно две задачи.

2. Изучение нового материала.

1) Определение сферы и шара (на моделях и рисунках) №574 (а).

2) Уравнение сферы.

3) Решение устных примеров.

3. Закрепление материала. № 576 (а), 576 (б)-С, 578 (г), 577 (а), 579 (а, б)

4. Домашнее задание: параграф 3. П 58,59. №576 (б), 577 (б), 579(в, г), 574(б).

5. Итог урока.

6. Решение задач повышенной сложности.

Ход урока

1) Организационный момент

2) Проверка домашнего задания.

3) Учитель: Ребята, вам на дом было повторить определение окружности, круга, расстояние между двумя точками в пространстве. Уравнение окружности.

Показываю плакат окружности, круга и повторяем определение.

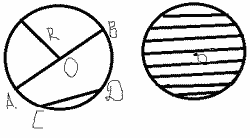
Ученики:

Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.

Круг – часть плоскости, ограниченная окружностью.

Учитель: Напишите, пожалуйста, на доске уравнение окружности (x-x₀)²+ (y-y₀)² = R², где (x₀; y₀)- центр окружности, R- радиус, (x; y)- координата центра окружности.

Устно. Найти уравнение окружности?

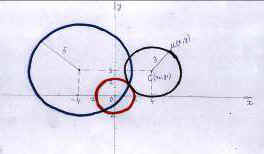
1) (x-4)²+(y-3)² =9. 2) x²+ y²=4. 3) (0-4)²+(0-3)²=R². 4) 16+9=R².

5)25=R² . 6) R=5. 7)(x+4)² +(y-3)² =25.

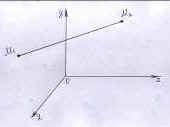
Учитель: Найдите расстояние М₁ М₂, если М₁ (-3; 0; 4), М₂ (0; 6; 5). М₁ М₂= (0-3)²+ (6-0)² +(5-4)² = 46.

Следовательно, d= (x-x)² +(y-y)²+ (z-z)².

12 3 Следующая ⇒