Решить самостоятельно.. Пример№5.. Решить самостоятельно.. Решить самостоятельно.

Решить самостоятельно.

Пример№5.

Найти область определения

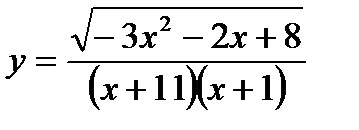
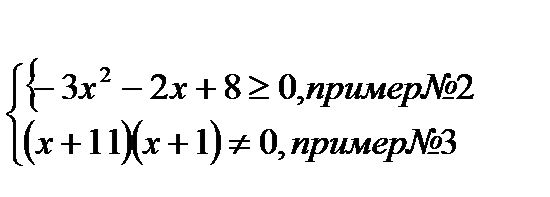
-3х² -2х +8 ≥ 0

-3х² -2х +8 = 0

Д = 100

х₁ = -2 и х₂ = 8/6 или 4/3

Разбиваем на интервалы и определяем знаки, ответом будет [ -2; 4/3]

- -2 + 4/3 -

——☻——☻——

Решаем:

х + 11 ≠ 0

х ≠ -11

х + 1 ≠ 0

х ≠ -1

Из полученного интервала убираем х = -1, х = -11 в нем нет

Ответ: Д(у) = [ -2; -1)(-1; 4/3]

Решить самостоятельно.

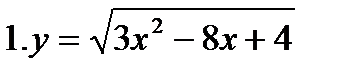
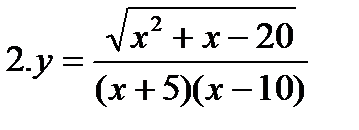
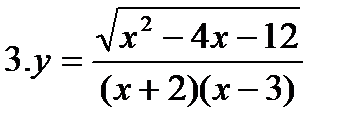
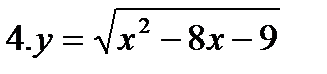
Пример №6. Найти область определения у = log₅ (х² - 4х + 3)

Областью определения логарифмической функции являются только положительные числа.

Поэтому не обращаем внимание на основание и что написано под знаком логарифма , всегда пишем, что выражение больше 0: х² - 4х + 3 > 0

Решаем квадратное неравенство через дискриминант, метод интервалов, ответ только со знаком плюс, скобки круглые.

Д = 4, х₁ = 3 и х₂ = 1

+ 1 - 3 +

————— —

Ответ: (-∞; 1) (3; +∞)

Решить самостоятельно.

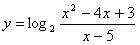
Применяем метод интервалов.