Задания для подготовки к экзаменам

Стр 1 из 2Следующая ⇒

Задания для подготовки к экзаменам

Тема №1. Метод интервалов.

Пример №1. Решить методом интервалов: х^{2 _} 3х + 2 ≤ 0

Алгоритм.

1. Приравниваем к нулю и решаем квадратное уравнение

Д = 9 - 2• 4 = 1; х₁= 1; х₂= 2;

2. Разбиваем на интервалы и определяем знаки на интервалах

+ 1 - 2 +

───☻─────☻─────

↑0

3.Записываем ответ: [1; 2]

Пример №2. Решить методом интервалов:

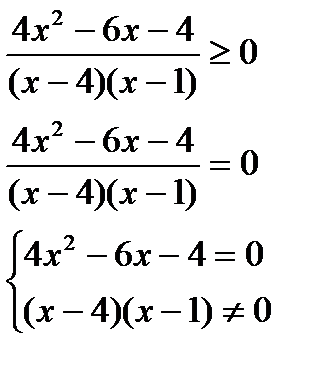
Числитель равен нулю, знаменатель нулю не равен.

Д = 100, х₁= 2, х₂ = -1/2

+ -1/2 - 2 +

───☻─────☻─────

Ответы будут со знаками плюс.

Решаем второе уравнение: х₃≠ 4 и х₄ ≠ 1.

В полученные интервалы входит число 4, исключаем его.

Ответ: х ϵ (-∞; -1/2] U [2; 4) U (4; +∞)

Решить самостоятельно.

Тема №2: Область определения функции.

Определение: Областью определения функции, заданной формулой - называется множество значений переменной х, при которых действия, записанные формулой выполняются.

Пример №1. у = х² + 4х + 5

Все действия, записанные в формуле выполняются.

Ответ: Д(у) = (-∞; +∞)

Пример №2.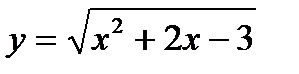

Корень квадратный не существует из отрицательных чисел

х² + 2х - 3 ≥ 0

х² + 2х – 3 = 0

Д = 4 – 4∙ 1 ∙(-3) = 16

х₁= 1 х ₂= -3

Разбиваем на интервалы, определяем знаки на интервалах

+ -3 - 1 +

——☻——☻——

Ответ: Д(у) = (-∞; -3] U [1; +∞)∙

Пример №3.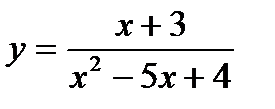

На нуль делить нельзя

х² – 5х + 4 ≠ 0;

Д = 25 – 4 ∙1 ∙4 = 9;

х₁ ≠ 4; х₂≠ 1.

Записываем ответ: все числа, кроме 1 и 4

Ответ: Д(у) = ( -∞; 1)U( 1; 4)U( 4; +∞)

Пример №4. Найти область определения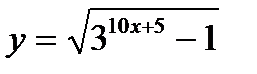

3^10х-5- 1 ≥ 0

Пример №2. Корень квадратный не существует из отрицательных чисел

3^10х-5 ≥ 1, перенесли 1 вправо, получили показательное неравенство. Метод уравнивания в обеих частях уравнения

1 = 3⁰

3^10х-5 ≥ 3⁰

10х - 5 ≥ 0

10х ≥ 5

х ≥ 1/2

Ответ: Д(у) = [1/2; +∞)

12 Следующая ⇒